→ Pay attention
Before contest
Rayan Programming Contest 2024 - Selection (Codeforces Round, Div. 1 + Div. 2)
5 days
Register now »
Rayan Programming Contest 2024 - Selection (Codeforces Round, Div. 1 + Div. 2)
5 days
Register now »
*has extra registration
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3993 |
| 2 | jiangly | 3743 |
| 3 | orzdevinwang | 3707 |
| 4 | Radewoosh | 3627 |
| 5 | jqdai0815 | 3620 |
| 6 | Benq | 3564 |
| 7 | Kevin114514 | 3443 |
| 8 | ksun48 | 3434 |
| 9 | Rewinding | 3397 |
| 10 | Um_nik | 3396 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
→ Find user
→ Recent actions
↑
↓
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Nov/25/2024 10:08:45 (j3).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|











Remainder: Contest starts in less than 15 minutes.
How to solve D (Hokej)?
I guess the sufficient condition is that:
t[i] is the time of i-th player plays.
1.0 ≤ t[i] ≤ M.
2.sum(t[i]) = 6 * M.
I think the following greedy works, but I don't have proof: let's sort the players by quality. Then make a 6 × n table (so it has 6 rows and n columns) and from left to right fill it greedily with players not exhausting their endurance. From this matrix calculate the needed things.
Greedy: let the most skilled players go on the field.
For constructing the solution, treat the player slots as a rectangular table of 6 rows and M columns, and fill the players into the table from left to right and from top to bottom one by one, in decreasing order of their quality. Since each player takes up no more than M cells, this is sure to give a valid solution within 2N substitutions.
Upd. My program gets "Illegal substitute" on the last four tests, but I suppose the sketch remains correct...
How long until final results?
Results are out!
How to solve C for 100pts? I thought about trie or hashing but couldn't implement it.
Insert all passwords into a trie and then use bruteforce to check every substring of every password.
For storing strings use unordered_map which is basically hashing
Simple std::map passes too. I stored count of strings in a map, checked every substring of every string, and multiplied by the counts. It results in O(NM2log(N)) complexity, where M is the length of the strings, so about 3 * 107 operations. My solution passed with 0.49 s on worst case.
Why doesn't Nlog^2 N solution pass in E? (binary search + segtree) Also, what's the intended solution?
I coded such a solution and got full points (slowest time 0.46s). Code
Seems is intended. Sort the events and queries offline by values of x (number of stops) and process the remaining dimension (children's age) with a segment tree.
is intended. Sort the events and queries offline by values of x (number of stops) and process the remaining dimension (children's age) with a segment tree.
I did O(nlogn) with online queries.
I use a segment tree, where the base nodes are the children, and the values are the currently assigned drop off (INF by default). The upper nodes are min of their children. Updates are simple segtree updates.
When querying I move right, or right-up (i. e. from v either to v + 1 or to v / 2. When I can't move neither way, or I reach a node with at most Y value, I stop. If the stop node's value is bigger than Y, then the answer is -1. Otherwise, I move left, leftdown or rightdown, (i. e. from v either to v - 1, v * 2 or v * 2 + 1) in this preferency order, such the node I move to, got value at most Y. When we reach a base node, it will be the optimal answer.
Here is my code.
Does anyone know what "Illegal substitute!" mean in D, because I can't find the error in my code.
It probably means you bring down and up the same person at one moment, which is illegal. So instead of a - > b you do c - > a, a - > b.
Do you remember the rule "but a player cannot enter the game, and then exit in the same moment, or vice versa"?
I don't think that this is the problem, I checked it with this checker (I hope it's correct :D): checker Also it shouldn't happen with my solution.
The test cases are open to download, so if you have time, and luck, you can check manually for something illegal. Or just send source code.
Oops the checker was buggy, my bad. It's really the problem :D Sorry.
Maybe there are bugs on lines 25 and 26.
Can anyone explain F solution?
I wasn’t able to participate, so this might get wrong
As the rectangles form a tree structure, our task is simplified to
If we do these fast, other stuffs are fairly easy.
We can use sweep line to do that. In a BST (std::set) we store rectangle as an interval, sorted in order of lower y coordinate. To build a tree, we just need to find a parent. This can be done by lower_bound operation in insertion phase (lower y coordinate slightly less than current interval). Query can be done in simillar way. So this is solvable in O((n+m)lgn)
You build a tree of the rectangles (they are the vertices). By this I mean that the parent of rectangle X is the smallest rectangle Y, which contains X inside of it. This can be done with sweep line on the X-axis using a segment tree for the Y-axis in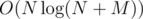 time.
time.
Now for every paintball ball we find the smallest rectangle containing it. After that we add that we have colored this rectangle with color of the given ball (we simply add it to a vector for this rectangle or something like that). This again can be done in with sweep line in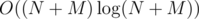 time.
time.
Well now we have a tree and some vertices already have colors for them. Well if we have colored vertex X in some color, all of its ancestors also are colored with the same color. From this we see that a rectangle (vertex) is colored with all colors in it's sub tree. This is a well known problem which can be solved in with a segment tree and DFS order or with "dsu on tree" (I used this).
with a segment tree and DFS order or with "dsu on tree" (I used this).
So the whole solution has running time of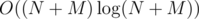 . Here is my AC code from the competition.
. Here is my AC code from the competition.
PS: In my code both sweep lines are merged into one.
I thought of the same thing, but I don't think you need to explicitly build a graph. You could create an array of sets
std::set<int> S[MAXN]containing the colours in rectangleS[i], and iterate the rectangles in increasing order of size, merging the current rectangle's set with its parent's at every step.