COCI 2017/2018 — Round 2

7 years ago, # |

+20

Very interesting problems)
How to solve E (Usmjeri) and F (Garaža)?

→ Reply

I_Love_Tina

7 years ago, # ^ |

← Rev. 6 →

+16

Root the tree. Let path a - b be p₁ = a, p₂, p₃, ..., p_k, ..., p_t = b where p_k is their lca. If k = 1 or k = t then all edges (p_i, p_i + 1), (1 ≤ i < t) must be either all directed down the root or all up the root. Suppose now this is not the case, then the edges (p_i, p_i + 1), (1 ≤ i < k) must have the same direction (down or up the root) and also the edges (p_i, p_i + 1), (k ≤ i < n) must have the same direction while the edges (p_k - 1, p_k) and (p_k, p_k + 1) must have different directions so now you obtained a simple 2-sat problem for which you can find if there is a solution in O(n) and the number of solutions is 2^{number of conex components in the 2 - sat graph}.

→ Reply

7 years ago, # ^ |

Oh 2-sat. Very beautiful solution.

→ Reply

7 years ago, # ^ |

Nice. Can you post your code, please?

→ Reply

I_Love_Tina

7 years ago, # ^ |

I'll post it after it gets AC.

→ Reply

szawinis

7 years ago, # ^ |

← Rev. 2 →

Mine is more or less the same big idea as I_Love_Tina's, but the details might be different. I only managed to finish coding after the contest was over :(

Here's my solution accepted in analysis mode (runs in 0.72s): Click

→ Reply

farmersrice

7 years ago, # ^ |

Can you please elaborate on how you check if the answer is 0? I am getting 4 wrong answers because my code thinks it's non-zero.

→ Reply

szawinis

7 years ago, # ^ |

If (v, 0) and (v, 1) are in the same component.

→ Reply

Noam527

7 years ago, # ^ |

I understood everything you said but I couldn't figure out during the contest just how I maintain the subsets of edges that should have the same direction. Mind explaining a little further?

→ Reply

I_Love_Tina

7 years ago, # ^ |

← Rev. 2 →

You will maintain edges in a compressed form. Let the k^th ancestor of vertex x be f[k][x]. You will maintain an array E[x][y] that is marked if all the edges on the path from vertex y to vertex f[2^x][y] are equal. Now if you have that all edges from vertex x to vertex f[k][x] are equal then pick up the largest t with 2^t ≤ k and mark E[t][x] and E[t][f[k - 2^t][x]]. Now if E[t][x] is marked you can say that E[t - 1][x] and E[t - 1][f[2^t - 1][x]] are marked and the edges (f[2^t - 1 - 1][x], f[2^t - 1][x]) and (f[2^t - 1][x], f[2^t - 1 + 1][x]) have the same direction. This way you can reduce the edges in $\text{[math]}$ .

→ Reply

zadrga

7 years ago, # ^ |

← Rev. 2 →

How can you check if answer is 0? And also what are variables in 2-SAT problem (what do variables represent in our task)? I have never solved any 2-SAT problem, so I would really appreciate more detailed description of solution?

→ Reply

7 years ago, # ^ |

hint for F (it can be solved with different data structures after that):

Imagine we change the value of position i. Let's find the leftmost position j such that gcd(j, i) = a_i (here gcd(l, r) is the GCD of the range a_l, a_l + 1, ..., a_r). Now we know that the gcd(j - 1, r) will decrease. Well let's find the leftmost position j₂, such that gcd(j₂, i) = gcd(j - 1, i).

If we do this until gcd(j_k - 1, i) = 1 how many such ranges can we have in worst case?

Well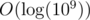 $\text{[math]}$ .

→ Reply

7 years ago, # ^ |

I already knew that fact. But I have no idea what to do next.

→ Reply

7 years ago, # ^ |

← Rev. 4 →

+15

Well if we had no updates we could solve the problem like that:

For every position i find rightmost position r_i such that gcd(i, r_i) > 1.

Now the answer for a query [L;R] is ( (sum of r values in [L;R]) — (sum of r values in [L;R] greater than R) + (count of r values in [L;R] greater than R) * R — R * (R + 1) / 2 + (L * (L - 1) / 2)).

Well this can be done with a merge sort tree in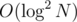 $\text{[math]}$ .

Now how to handle updates?

Well we go through the O(log(10⁹)) ranges from the previous comment. Now with binary search in segment tree we find for each of the ranges the corresponding r value. You can see that this r value will be the same for all of the positions in a given range. Well now we simply set the values in the range to r.

The data structure we will use will be merge sort tree with treap in every node, because using it the set operation of an interval can be done easily.

The complexity will be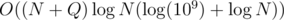 $\text{[math]}$ .

→ Reply

7 years ago, # ^ |

← Rev. 4 →

You can see that this r value will be the same for all of the positions in a given range.

How to understand this?

UPD Understood. Thanks. But I guess treap is too heavy and, probably, a simpler solution exists.

→ Reply

7 years ago, # ^ |

Well time limit is 4 sec so this should fit in TL without a problem.

Another possibility is to use SQRT decomposition (if you don't like treaps :D) and get a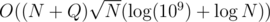 $\text{[math]}$ solution which also should pass if implemented well.

→ Reply

dragoon

7 years ago, # ^ |

I think your solution is too complex. With one more observation, you can simplify your solution a lot.

Suppose, f(i) = maximum index j, such that gcd[i, j] > 1. Note that, f(1) <= f(2) <= ...

So for a query, [L, R], you can binary search and find, largest i (L <= i <= R) such that, f(i) <= R. Then rest is just application of simple segment tree.

→ Reply

7 years ago, # ^ |

Oh nice. I feel stupid now :D

→ Reply

cheater2k

7 years ago, # ^ |

How can you calculate j₁, j₂, ...? I cannot find a suitable time complexity to solve this. I only know a O(log(10⁹) * log(N)²) solution per update by using a segment tree of GCD and binary search. However, it seems that such a solution is not fast enough to pass the testcases.

→ Reply

7 years ago, # ^ |

← Rev. 2 →

OPS I explained how to find the closest position to the right, not to the left, but the idea to find the one to the left is basically the same.

You do the binary search inside the segment tree:

Let's get the nodes in the segment tree which the query [i;N] will cover. They will obviously be at most $\text{[math]}$ . Now we begin from the leftmost such interval and go through these nodes.

If the interval of the current node is [L;R] we can easily find gcd(i, R) in O(1) using the gcd values of the previous intervals.

We find the first interval, such that gcd(i, R) = 1. This will be done in $\text{[math]}$ time.

Well now we know that the position which we are searching for (current j) is in a given interval [L;R] (we also know the number of this node in the segment tree).

Well we just start going down from our current node:

If the GCD of the current gcd and the gcd of the left child is not 1, we go to the right child with the new gcd. Else we go to the left child with the same gcd.

Using this in the end we will be at the first position x with gcd(i, x) = 1. The complexity will be $\text{[math]}$ .

So overall complexity for finding the closest position to the right of a given position will be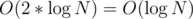 $\text{[math]}$ .

→ Reply

TahsinEnesKuru

7 years ago, # ^ |

In Problem E I found solution with HLD. But i haven't coded HLD before. So i can't.

My Solution

Am i wrong ? Sorry for my bad English :D

→ Reply

7 years ago, # ^ |

I've had something like that. But without hld. I even have code, but it doesn't work. It seems to be correct.

→ Reply

TahsinEnesKuru

7 years ago, # ^ |

i found my mistake. But it will work

→ Reply

7 years ago, # |

← Rev. 2 →

Yeah, nice problems

How to solve C? I solved D with meet-in-the-middle but not C :P

→ Reply

Len

7 years ago, # ^ |

← Rev. 3 →

You only need to consider subarrays that if you reverse it one of its endpoints will become fixed point. So only o(n) subarrays to check.

→ Reply

7 years ago, # ^ |

← Rev. 2 →

Yes, $\text{[math]}$ subarrays to check. But, every subarray is checked in $\text{[math]}$ , no? Am I blind? :D

UPD No question anymore.

→ Reply

7 years ago, # ^ |

← Rev. 3 →

What about N, N - 1, ..., 1 test?

UPD No question anymore.

→ Reply

MladenP

7 years ago, # ^ |

← Rev. 2 →

For each i, calculate i+a[i], and put it into buckets. The number of fixed points in the flipped subarray [L, R] is the number of indices between L and R that are in bucket L+R. (you can use binary search). You can see it in my code that I posted down.

→ Reply

Len

7 years ago, # ^ |

← Rev. 4 →

r — (i — l + 1) + 1 = p[i]
r — i + l — 1 + 1 = p[i]
r + l = p[i] + i
also don't forget about fixed points that are not inside [L,R]

→ Reply

7 years ago, # ^ |

← Rev. 2 →

Can you describe this point in more details, please? :)

UPD Undestood. Good :)

→ Reply

Joxa_P

7 years ago, # ^ |

Calculate prefix sum of elements that are at begining in right position. For every element x there is only one y (element or position between 2 elements) so one of the options is to reverse array around y where x is last element we reverse.Now for every y we try solutions and possible x are sorted (you processed from 1 to n) so just iterrate that list and substract number of elements that are at right position in that interval.

→ Reply

KieranHorgan

7 years ago, # ^ |

That is what I implemented but I didn't think it would pass with N up to 500,000. How did you go about checking each of the O(n) subarrays?

→ Reply

MladenP

7 years ago, # ^ |

← Rev. 3 →

This is what I did, I think it's correct: Basically, it only makes sense to swap [L, R] if a[L] = R or a[R] = L, therefore you only have N subarrays to check. codeEdit: too late :P

→ Reply

giorgosgiapis

7 years ago, # |

How to solve D? I guess it is solved using meet-in-the middle but couldn't figure out the solution.

→ Reply

MladenP

7 years ago, # ^ |

+14

You keep an array of pairs for the first half {sum, height of last one}, and for the second you do {sum, height of first one}, then you place the second ones into buckets based on height, then using binary search you find out how many will make a sum over K.

→ Reply

7 years ago, # ^ |

Like this: https://pastebin.com/64uCcnfC

→ Reply