Hi CF!
I was recently solving this problem : http://www.spoj.com/problems/KOPC12B/
The problem statement is just one line, so no need to rephrase it.
Knowing the solution to the problem without weights, and printing consecutive values, I guessed the answer to be n*C(2n,n)/2 after some trial and error and was surprised it passed.
I tried to arrive at a combinatronics proof by trying to pose the problem as counting binary strings with certain properties, but didn't get somewhere noticeable, I also tried changing (C(n,k)^2) to C(n,k) * C(n,n — k).
Any help proving this? Thanks.










Let's first find
The sum in the problem can be obtained by differentiating the above.
Consider the following expansion:
Notice that if you square the right side, S(x) can be obtained by taking the half coefficient of y^n. So we find the coefficient of y^n in square of left side, hence,
Add the (n choose 0) term with weight 0 to the sum. Notice that reversing the weights gives the same sum. Adding them term-by-term will get you weights equal to n everywhere, exactly like in the young-gauss-outwits-teacher anecdote. And this brings you to the unweighted version, which has a nice combinatorial interpretation.
There is a known formula that . That's because if we want to choose n people out of n boys and n girls we can firstly fix number i and then choose i boys and n-i girls. Multiplying
. That's because if we want to choose n people out of n boys and n girls we can firstly fix number i and then choose i boys and n-i girls. Multiplying 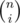 by i accounts for choosing a leader out of boys (or girls if you prefer :p). Equivalently we can choose n people and then choose leader — in half of cases leader will be a boy which expresses RHS.
by i accounts for choosing a leader out of boys (or girls if you prefer :p). Equivalently we can choose n people and then choose leader — in half of cases leader will be a boy which expresses RHS.
Yes I knew the first part from Vandermonde's identity. I still have to say the leader part is so smart yet simple! Thank you :). Do you know of similar problems? :p
Thanks as well to other people who responded.
Yes, I have: http://agc013.contest.atcoder.jp/tasks/agc013_e and https://drive.google.com/file/d/0B7XFjfP_Zx_RRy1nMno3WU4tY2s/view?usp=drive_web
I did both of them in similar way as this identity , adding some features to every "group" to get corresponding multipliers
Awesome!
Thanks again.
We can also evaluate it by finding the coefficient of x^0 in product of ((1+x)^n)*((1+1/x)^n)=((1+x)^2n)/x^n. Coefficient of x^0 is equal to 2nCn.