YogayoG's blog

The number of Partition of an Integer
By YogayoG, history, 7 years ago, In English

Hi Everyone.

Now I'm wondering how to find the number of partition of an integer N(<=10^5).

Any advice?

The number of partition of 4 is 5.

4 = 4.

4 = 3 + 1.

4 = 2 + 2.

4 = 2 + 1 + 1.

4 = 1 + 1 + 1 + 1.

Thank You.

  • Vote: I like it
  • +8
  • Vote: I do not like it

»
7 years ago, # |
  Vote: I like it +5 Vote: I do not like it

Auto comment: topic has been updated by YogayoG (previous revision, new revision, compare).

→ Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it +20 Vote: I do not like it

I came up with following solution. It uses the fact that either minimal summand in the partition or ammount of summands is not too big. Let arrange the summands in the partition in the non decreasing order. Denote f(i, j) — number of partitions of number i if the minimal summand is j, g(i, j) — number of partitions of number i if the amount of summands is j. Then f(i, j) = f(i - j, j) + f(i, j + 1) (we either put j as a new summand or increase the minimal summand), g(i, j) = g(i - 1, j - 1) + g(i - j, j) (we either put 1 as a new summand or we will have all the summands are greater than 1 then decrease all of them by 1 and return to the state when all the summands are greater or equal than 1). Let p be such number that (p - 1) * (p - 1) ≤ n, p * p > n. Let s = p - 1. We compute values of g(i, j) for all i = 1...n, j = 1...s. Then lets calculate values of f(i, p) for all i = 1...n. Iterate through the number of summand here and express it through the fungtion g: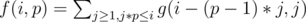 . Then we can calculate values of f(i, j) for all i = 1...n, j = 1...s. Time and space complexity are 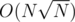. It seems pretty amazing to me that there is such a solution while before I encountered with such a problem and didn't know that it's possible to solve it with such complexity. Is it known that we can solve this problem with such complexity or better?

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +28 Vote: I do not like it

    You can also compute it using pentagonal numbers in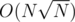 . It's a bit easier to implemenent, but much less intuitive than your solution.

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it +5 Vote: I do not like it

      bciobanu I have read that before. And I can't understand why it works. Thanks for pointing me that it's easier to implement, I will trying to understand it.

      → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +5 Vote: I do not like it

    Thank you ABalobanov for your solution. And seems your solution surely will pass the time limit.

    → Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it +10 Vote: I do not like it

On the OEIS page, the formula involving A001318 looks like it yields an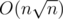 solution if addition and subtraction are O(1) (e.g., modulo an integer).

Edit: this is essentially the same as bciobanu's comment above.

→ Reply