Lance_HAOH's blog

Sort a list of integers by prime factorization
By Lance_HAOH, history, 7 years ago, In English

Hi. I am trying to solve this problem.

For convenience, I have replicated the problem statement below:

Given a list of N integers (non-distinct) where 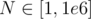and each integer 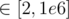, sort the integers based on the lexicographical order of their prime factorization.

Example (the first number is N):

5
2 3 4 5 6

Expected Output:

2
4
6
3
5

Explanation:

2 = 2
3 = 3
4 = 2 * 2
5 = 5
6 = 2 * 3

Time limit is 2s and memory limit is 32MB.

My attempt:

I used a fast factorization method to factor each integer into its prime factors and store them into a 2D matrix, M. M[i][j] represents the jth prime factor of the ith integer in the list such that M[i][j] ≤ M[i][j + 1].

Now, I use a custom sort method to sort the list. Let's say we want to compare integers at position u and v in the list.The sort function will compare M[u] and M[v] using lexicographical comparison.

My code.

This method is correct but it will get MLE (not TLE surprisingly). I tried asking this problem on stackoverflow but could not obtain a satisfactory answer. Could someone please advise me on a better way to solve this problem?

p.s. not sure if this info would be helpful — this problem is tagged with dfs in the source.

  • Vote: I like it
  • +8
  • Vote: I do not like it

Comments Comments (14)
| Write comment?
»
7 years ago, # |
← Rev. 3   Vote: I like it 0 Vote: I do not like it

I will use a typical sorting algo. something like a quicksort maybe. something like:

void quicksort(int start, int end, int prime_idx, int cum) {
  if(start == end) return;
     int i = (start - 1);
    //to handle case where arr[j]==1
    for(int j = start; j<=end; ++j) {
      if(arr[j]==cum) {
         swap(start,j);
         start++;
      }
    }
    for (int j = start; j <= end- 1; j++)
    {
        // 
        if (arr[j]%(cum*prime[prime_idx])==0)
        {
            i++;    // increment index of smaller element
            swap(arr[i],arr[j]);
        }
    }
    swap(arr[i+1], arr[end]);
    quicksort(start, i, prime_idx, cum*prime[prime[idx]]);
    quicksort(i+1, end, prime_idx+1, cum);
}

Beware this code is not tested and i havent written a quicksort in years. Also I am not sure about the complexity, but I believe it should be fast enough. EDIT: fix the arr[i]==1 part.

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    What does prime[prime_idx] contain?

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
      ← Rev. 4   Vote: I like it 0 Vote: I do not like it

      sorted prime factors

      EDIT: I didnt realize this is lexicographical sorted. I believe just storing the prime factors of all the elements in the array and store it lexicographically?

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Hmm. My original approach already attempts to sort the integers by lexicographical order of their prime numbers but it gets MLE. How does your approach avoid the MLE?

        → Reply
        • »
          »
          »
          »
          »
          7 years ago, # ^ |
          ← Rev. 3   Vote: I like it 0 Vote: I do not like it

          I am not fully sure why your approach use so many memory. You can see that my quicksort approach only use constant memory each call, which makes it fine. and my prime vector is small as there is at most 1000000 primes from 1 to 1e6? so how would it MLE?

          EDIT: I see why your MLE now, you use N*21 arrray to store your factor, which is too high for the tight constraint given.

          → Reply
          • »
            »
            »
            »
            »
            »
            7 years ago, # ^ |
              Vote: I like it 0 Vote: I do not like it

            If I understood correctly, your approach will perform trial division on each integer in the list. There are about 78000 primes less than 1e6. So that means that we will do 78k * 1e6 operations. Am I right?

            → Reply
            • »
              »
              »
              »
              »
              »
              »
              7 years ago, # ^ |
                Vote: I like it 0 Vote: I do not like it

              yes, indeed i blundered.

              Sorry, after thinking through. Create a trie/graph. For each element, store it base on the prime factor. After that transverse the trie and get the number one by one base on the order.

              The memory should be O(number of prime factor * depth), which should be small enough.

              → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

If your comparison function works in you don't need to waste memory on storing the factors, you can factor the numbers while comparing them.

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Hmm. That's interesting. How would you compare two integers by their prime factors in O(logn)?

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      The same way you extracted the prime factors themselves

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        That means I must simultaneously factor all the integers at once?

        → Reply
        • »
          »
          »
          »
          »
          7 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          No, I meant, something like this:

          bool cmp(const int i, const int j) {
	int x = a[i];
	int y = a[j];
	while (x != y) {
		int p = lowestDiv[x];
		int q = lowestDiv[y];
		if (p != q) {
			return p < q;
		}
		x /= p;
		y /= q;
	}
	return false;
}
          → Reply
          • »
            »
            »
            »
            »
            »
            7 years ago, # ^ |
              Vote: I like it +9 Vote: I do not like it

            Got AC with this trick! Thanks so much for this short and simple solution!

            → Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it +1 Vote: I do not like it

Here's a nice solution:

First I'll denote the elements limit by lim. Find all the prime numbers from 1 to lim using sieve.

Now, we will make a vector keys of size lim + 1. every number X from 1 to lim will have in keys[X] a value, which is its location if we sorted all numbers from 1 to lim by the lexicographical order of their prime factorization (that is, 1 will have key 1, 2 will have key 2, 4 (2 * 2) will have key 3...).

To do this, we will create all the prime factorizations by lexicographical order. That is, we will first create all those that are just with 2's, then we will invlove 3 in the prime factorization, and so on. For instance, the first numbers we will go through are:

1, 2, 4, 8, 16, ...., 524288 (2^19), 786432 (2^18 * 3^1)...

The way to do this is with a very simple recursion: we will maintain the current value we're on, and the last prime factor we took. then, we go through all the primes from the last prime we took, until the end of the vector, or until (the current prime we're on) * (the current value in the recursion) is bigger than lim.

We maintain the last prime factor since we don't want things like this to happen: 12 = 2 * 3 * 2. (This is just by the definition of the prime factorization — we go by the increasing factors.)

The above can be proved to run in O(lim), and gives us a comparison function that works in O(1) (we just compare keys).

Here is a sample code:

const int lim = 1e6;
int n, nextkey = 1;
vector<int> a, p, keys;

void sieve() {
	vector<bool> b(1e6 + 1, true);
	int i = 2;
	for (; i * i < b.size(); i++) {
		if (b[i]) {
			p.push_back(i);
			for (int j = i * i; j < b.size(); j += i) b[j] = false;
		}
	}
	for (; i < b.size(); i++) if (b[i]) p.push_back(i);
}

void calc(int val = 1, int lastind = 0) {
	keys[val] = nextkey;
	nextkey++;

	while (lastind < p.size() && (long long)val * p[lastind] <= lim) {
		calc(val * p[lastind], lastind);
		lastind++;
	}
}

bool cmp(int &a, int &b) {
	return keys[a] < keys[b];
}

int main() {
	keys.resize(lim + 1);
	sieve();
	calc();

	cin >> n;
	a.resize(n);
	for (int i = 0; i < n; i++) cin >> a[i];
	
	sort(a.begin(), a.end(), cmp);

	for (auto &i : a) cout << i << " "; cout << endl;
}

This works in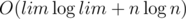 . (Note that you can also make the sorting in O(n) using countsort, because the keys are between 1 and lim).

→ Reply