Given a list of n numbers in which all but one repeat exactly k times, but the remaining one appears less than k times (and at least once).
Find this number (which repeats less than k times).
Expected Complexity
Time ≤ O(nlgk)
Memory ≤ O(lgk)
→ Обратите внимание
→ Трансляции
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 3985 |
| 2 | jiangly | 3814 |
| 3 | jqdai0815 | 3682 |
| 4 | Benq | 3529 |
| 5 | orzdevinwang | 3526 |
| 6 | ksun48 | 3517 |
| 7 | Radewoosh | 3410 |
| 8 | hos.lyric | 3399 |
| 9 | ecnerwala | 3392 |
| 9 | Um_nik | 3392 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 169 |
| 2 | maomao90 | 162 |
| 2 | Um_nik | 162 |
| 4 | atcoder_official | 161 |
| 5 | djm03178 | 158 |
| 6 | -is-this-fft- | 157 |
| 7 | adamant | 155 |
| 8 | awoo | 154 |
| 8 | Dominater069 | 154 |
| 10 | luogu_official | 150 |
→ Найти пользователя
→ Прямой эфир
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 23.12.2024 04:10:32 (f1).
Десктопная версия, переключиться на мобильную.
При поддержке
Use quicksort to sort in nlogk and then traverse array to find element which occurs less than k times in O(n).
Storing the elements of list would require O(n) memory!
Use in place quicksort to do it in O(lgn)
See this thread — https://apps.topcoder.com/forums/?module=Thread&threadID=753840&start=0&mc=7
You cant read the elemenets into an array, the memory complexity O(lgk) I mentioned is strict, it does not mean extra space complexity.
Can you give me the source of the question ??
I am not sure but i think you can xor each number in base k to get the solution. It takes O(logk) memory. And O(n*logk) time complexity if you consider xor as constant time operation.
Yes, this was my intended idea. But the problem is at the end of xoring in base k, we will get the ans only if it repeats once. (however it can repeat [1, k) times)
I think this may be done in O(klgk considering k<n it still remains nlgk). After finding the answer see if it can be expressed as xor of a same number 1,2,...,k-1 times. Of course I am not sure of this one also.
Hint: for k = 2 we have the classical 'xor all elements' problem. Xorring m-bit numbers is just adding vectors in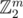
. Can you generalize this?
EDIT: I am assuming here that the number of bits is considered O(1).
Yes, it can be generalized to xor base k, but the issue that does not arise in k=2 case is that number is present exactly twice or exactly once, which greatly simplifies the problem (the answer is just xor of all numbers),
but for general k, how do we retrieve the number which repeats greater than 1 time and less than k times?
The number repeats 1 ≤ i < k times, so all positions in the final vector will have their value set to 0 (this bit is turned off in the required number) or to i (this bit is turned on in the required number).
For each bit store the value modulo k. Get the number, divide it by (n%k).
What if the coefficient of (n%k) is divisible by k, we wouldnt be able to retrieve in that case, right?
n % k < k, it represents number of occurences of required number
lets say n=6, k=4,
and list is [3, 3, 3, 3, 2, 2],
how will your approach work?
bit 1 -> 4 -> 0(modulo k)
bit 2 -> 6 -> 2(modulo k)
num = 4, divide it by (6%4) -> answer is 2