897A — Scarborough Fair By webmaster
For every i in range [l, r], if ci is c1 then change it into c2...
Because n, m are all very small, O(nm) can easily pass it.
PS. You can use binary search tree to solve it in 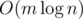 time.
time.
897B — Chtholly's request By webmaster
The k-th smallest zcy number is conn(str(k), rev(str(k))), where str denotes the decimal representation of a positive integer as a string, conn denotes the concatenation two strings, and rev denotes the reverse of a string.
Then go over the smallest k such numbers and sum them up to obtain the answer.
896A — Nephren gives a riddle By webmaster
f(n) = str1 + f(n - 1) + str2 + f(n - 1) + str3.
First we can compute the length of f(n) for all possible n.
For a pair of (n, k), we can easily determine which part the k-th character is in.
If it's in f(n - 1), we can solve the problem recursively.
The complexity of this algorithm is O(n), which is sufficient to pass all tests.
Obviously, length(f(n)) ≥ length(f(n - 1))·2, so length(f(60)) ≥ kmax.
It means that for all n > 60, the k-th character of f(n) can only be in str1 or the first f(n - 1).
Then we can answer a query in 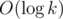 time.
time.
896B — Ithea Plays With Chtholly By dogther
As the initial sheet "has already" in a non-decreasing order (although it has no numbers), what we should do is just "maintain" this order.
We use a simple method to do so: find the first sheet whose number is strictly greater than the given number (or it's an empty sheet) and replace it with the new number.
For each round, we either replace an existing number with a strictly smaller one, or fill in an empty sheet. The first case will happen at most c - 1 times for each sheet, and the second case will happen only once for each sheet. Thus in total, we will modify a sheet for at most c times. Thus, the total rounds won't be more than n × c.
To pass all the tests, we only need to maintain 2 similar sequences, one non-decreasing from the first and one non-increasing from the last, which makes a total round of  , precisely, and use binary search or brute force to complete the "finding" process.
, precisely, and use binary search or brute force to complete the "finding" process.
896C — Willem, Chtholly and Seniorious By ODT
This is an interesting algorithm which can easily deal with many data structure problems------if the data is random...
I initially named it as "Old Driver Tree" ( Which is my codeforces ID ).
(But now I call it Chtholly Tree~).
We can find that there is an operation that makes a range of number the same.
We can use an interval tree (std::set is enough) to maintain every interval that consists of the same number.
And for operation 2, we destory all the intervals in range [l, r] , and put in a new interval [l, r] into the interval tree.
For operations 1, 3, 4, we can brute-forcely walk on the tree, find every interval in range [l, r], and do the required operation on it.
Proof of time complexity:
We suppose that we have a randomly selected range [l, r] now, and we randomly choose which operation it is, suppose that there are x intervals in this range.
1/4 possibility we use O(x) time to erase O(x) nodes.
2/4 possibility we use O(x) time to erase nothing.
1/4 possibility we use O(x) time to erase nothing and add 2 new nodes into the tree.
So we are expected to use O(x) time to erase O(x) nodes.
By using interval tree to maintain, the time complexity of this problem is 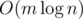 .
.
If operation 3 and 4 are changed into output the sum of ai for every i range [l, r], it seems that the time complexity may change into 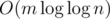 , but I do not know how to prove it...
, but I do not know how to prove it...
896D — Nephren Runs a Cinema By dogther
First let's consider a simpler problem that there are no customers with VIP cards and there are no 50-yuan notes left. For convinence, we suppose that n is an even number. The situation that n is an odd number will be similar.
By defining points (number of customers currently, number of 50-yuan note left) on a 2d-plane, the answer to our second question is the ways of drawing lines from (0,0) to (n,0), such that two adjacent points' y-axis have a difference of 1, and that all the points are above the x-axis.
The total routes will be Cnn / 2, but some of them are invalid. Consider another route starting from (0,-2).
For each invalid way in the previous route, consider the first point (x,y) that y<0 (y=-1).
By creating a symmetry route with y=-1 for the route before this point, this route will become exactly one route starting from (0,-2), and every route starting from (0,-2) will become an invalid route in a similar way.
So the number of invalid routes is Cnn / 2 - 1 (that is the number of routes from (0,-2) to (n,0)). Thus the answer will be Cnn / 2 - Cnn / 2 - 1.
Similarly if there are [l,r] 50-yuan notes left, the answer will be Cnn / 2 - r / 2 - Cnn / 2 - l / 2 - 1.
Now let's enumerate how many customers are there with VIP cards. If there are i of them, the answer will time a factor Cni.
One last question is about the modulo number. First separate it into forms like (p1a1) * (p2a2)... where p1... are primes. We can calculate how many factor pi are there in (j!), and the modulo value of the remaining ones.
Each time we take out a facter pi in (j!), and it becomes some product of numbers that are not divisble by pi as well as a remaining part (j / pi)!. For example, we want to calculate the number of factor 3 in (16!), and the product of numbers that are not divisble by 3 in (16!) mod (3^2). Then we have:
16! = (1 * 2 * 4 * 5 * 7 * 8 * 10 * 11 * 13 * 14 * 16) * (1 * 2 * 3 * 4 * 5) * (3^5)
The first part are not divisble by 3, so we can calculate their value (mod 3^2) in advance, the second part is a smaller problem (5!), so we can solve it recursively. For the number of factor 3, just add 5 in this case and solve it recursively.
After calculating how many factor pi in (j!) and the modulo value of the remaining ones, we can calculate the combnation numbers correctly. Finally use Chinese Remainder Algorithm to combine them.
896E — Welcome home, Chtholly By ODT
I'm really sorry for letting the brute force algorithm pass the tests...
My code uses about 600ms, in order to let some algorithms with large constant or larger time complexity ( like 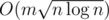 ) pass, I set the time limit to 3000ms.
) pass, I set the time limit to 3000ms.
The most naive brute forces uses about 8000ms to 9000ms, I added some tricks and the fastest can pass the tests in 5600ms.
In all the contests I've attended, pragma GCC was not allowed to be used...
But on codeforces, this can optimize brute force algorithm from 5600ms to about 2500ms...

Thanks to MrDindows and Shik for teaching me this lesson...
My solution to this problem:
Split the array into 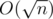 blocks, each containing
blocks, each containing 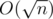 numbers.
numbers.
In each block, for example block x, use f[x][v] to represent the number of v in block x.
For each number i, belong[i] is the the block that i is in.
We need to maintain each number in the block.
This can be maintained by using DSU or linked list.
By maintaining this, we can get the value of every number in a block in 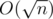 time.
time.
Notice that this two operations are the same:
1.For every number that is bigger than x, decrease it by x
2.Decrease every number by x, and for every number that is less than 1, increase it by x
For operation 1:
We get the value of each number in block belong[l] and belong[r] using the DSU or linked list, then for every number that should change, we change them.
Then we build block belong[l] and belong[r] up again.
For blocks numbered from belong[l] + 1 to belong[r] - 1:
If x × 2 ≤ max value in block p We merge all the numbers in range [1, x] to [x + 1, x × 2], and add x to tag[p] , tag[p] means that all the numbers in block p has decreased by tag[p].
If x × 2  max value in block p We merge all the numbers in range [x + 1, maxvalue] to [1, maxvalue - x].
max value in block p We merge all the numbers in range [x + 1, maxvalue] to [1, maxvalue - x].
For operation 2:
We get the value of each number in block belong[l] and belong[r] using the DSU or linked list.
We only need to traverse all the numbers in blocks belong[l] and belong[r], and traverse all the blocks between belong[l] and belong[r].
For block i in range [l, r], f[i][x + tag[i]] is the number of x in block i, so we just need to add this into the answer
Proof of time complexity:
There are 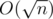 blocks.
blocks.
The difference between the max number and the min number in each block is initially n. So the sum of this in every block is 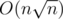 .
.
For each operation 1, we use O(x) time or O(max - x) time to make the difference of max and min element O(x) or O(max - x) smaller.
For each operation 2, we traverse 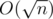 numbers and
numbers and 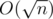 blocks.
blocks.
So the total time complexity if 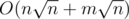
There seems to be another algorithm with the same time complexity, and has a smaller constant, but I couldn't prove its complexity so I used this algorithm instead.

(The missing picture on Div. 1E)
If you don't like it, just skip it please.










Auto comment: topic has been updated by ODT (previous revision, new revision, compare).
Auto comment: topic has been updated by ODT (previous revision, new revision, compare).
Thanks for the anime tho :p I am watching it and really enjoy it
I like the anime SukaSuka too.It's really great.
Second. We are going to the Scarborough Fair.
me too, but it seen that many people dont
It seems that we don't need Chinese Remainder Theorem in Div.1 D.Just let k divide gcd(k,p) when pre-processing the factorials and the inversion of factorials of k and multiply them back when computing the combination numbers.And it will lead to an O(nk) solution,where k is the number of prime divisors of p,which is no larger than 9.It runs really fast in practice,just consuming 46ms. My submission
I'm really sorry for letting the brute force algorithm pass the tests, but I do not know how to prove it...
Notice that: There IS a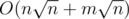 algorithm proved strictly. Meanwhile the brute force is strictly O(mn), only with a few computer architecture optimaztions that are not allowed on lots of other testing evironments.
algorithm proved strictly. Meanwhile the brute force is strictly O(mn), only with a few computer architecture optimaztions that are not allowed on lots of other testing evironments.
How to solve question A DIV2 in O(mlogn) time??
Here is how I believe it is solved:
First you make a (binary search) tree with each index of the segment as a leaf. Thus a tree of height n can store 2^{n-1} indexes. There are a linear number of nodes in the tree relative to the leaves (n-1 to be exact). Thus, traversing the worst case (the whole tree) takes linear time. But note that this tree stores an exponential amount of indexes. Traversing an exponential amount of space in linear time is the same as traversing a linear amount of space in logarithmic time. Thus, each query takes O(log n) time, so with m queries the problem is solved in O(mlogn) time.
Edit: I'm stupid and confused two different n, this solution doesn't work.
I don't really get how you can use the traversal of a binary search tree so solve queries in O(log n) time, could you explain more / write pseudocode?
Sorry, I stupidly conflated two different n's in my answer, so my answer doesn't work. Now I'm lost as well, I don't see how there is no linear n term in the complexity since n terms must be inputted/outputted.
I think by Binary Search Tree, he meant self balancing binary search trees like Treap or Splay Trees. Idea with Implicit Treap is obvious.
Edit: Well, it seems like it isn't obvious actually.
Can you explain your solution?
Make a map from char to treap keeping the corresponding occurences.
Now to set all c1 equal to c2 in range you only need to slice treap [c1] from l to r and then merge this slice into treap [c2].
Isn't merging 2 treaps done in O(n1 log n1/n2)? How does that result in a final complexity of O(n+mlogn)?
Merging in implicit treap doesn't mean that.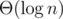
He meant keep a treap for each character and if you change a char c1 to c2, then cut the range [l, r] from treap of c1 and insert it into it's rightful place in treap of c2. That works in
But that's if the greatest value of one treap is smaller than the smallest value of the other treap.
If the first treap contains 1, 3, 5, 7, ... and the second treap contains 2, 4, 6, 8, ..., I don't see how it can be inserted.
Ya, you seem right. Thanks for pointing out :)
Well, the solution hence remains a mystery. Would anyone help? :D
Div1 C is interesting. For I had been lost in data structure :)
How to slove Div2 C and can somebody introduce me the similar problem?
When you look at the problem, you notice that the strings are defined recursively. Storing each string is infeasible, however, as each f_n uses f_(n-1) twice, and therefore takes up over double of the previous string's space. Thus, storing each string would quickly exceed the memory limit. As N is limited by 10^6 and Q is limited by 10, we see a linear query solution is sufficient.
To answer a query Q( n (string number), k (character number)) you need to check if the character is within the length of string f_n, these can be precomputed in linear time by iterating letting L[i] = min (L[i-1]*2+(added parts length), 10^18) (we don't need to know lengths above 10^18 due to our restriction on k.) As the editorial notes, we really only need to calculate this until n is 60.
Now that we are able to check if an answer exists, we need to actually calculate the answer. Each valid query asks for a character in one of five parts, the start of the string ("What are you doing..."), f_{n-1} , the middle of the string " Are you busy... " , f_{n-1} (again), or the end of the string ""?". If the query asks for a character in the start, middle, or end, the query can return that. Else, it returns a query on f_{n-1} (while adjusting which character it asked for by subtracting previous lengths.) This repeats until a character is found. (Note that the base case is at n=0, meaning it takes n recursions at most to solve.)
Thus we have a O(NQ) solution, which is acceptable.
In E-div2, Can someone prove how the randomization of l, r, op will result in the mentioned complexity? My intuition for it is weak and I can't imagne how the equal-value intervals will dramatically decrease.
After k merging operations, let's find the probability that index i is the right end of an interval. Note that number of right ends is same as number of intervals.
This happens iff all of the k merges either don't contain i or have i as the right end. There are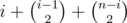 out of
out of 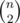 possible merges which satisfy this. So probability for k = 1 is
possible merges which satisfy this. So probability for k = 1 is 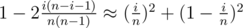 . And if we assume independence it's
. And if we assume independence it's 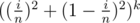 after k random merges.
after k random merges.
By linearity of expectation, expected number of intervals (right ends) is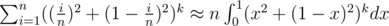 which is probably some small number I'll calculate later.
which is probably some small number I'll calculate later.
UPD: The number of segments is O(n / k), if someone wants a proof I can write it too.
Please provide proof for the number of segments. Thanks !
Sure thing :) It looks like I made a mistake, the correct answer is O(n / k) (edited above post) but the method stays the same.
Second to last line is a well-known identity obtained by expanding the binomial coefficient.
div 2 c,for string size of f(999) is more then long long int capacity.how to store it. also not getting this line"It means that for all n > 60, the k-th character of f(n) can only be in str1 or the first f(n - 1)"
For all n <= 54 you can store the string length, and for n >= 55, k won't pass the length of str1 loop,
How this pragma optimise works?
It tells GCC to replace optimization level specified in command line arguments with
Ofast.I can't understand Div. 2 D. Specifically the last paragraph.
P.S. Here, it's named 896 B Ithea Plays With Chtholly.
Our goal is to maintain two sequences, one starts from the beginning and the number of the sequence (from left to right) is non-decreasing, one starts from the end and the number is non-decreasing (from left to right). So after each round, the sheets look like this:
A1A2...Ar00...0B1B2...Bq
Here A1 ≤ A2 ≤ ... ≤ Ar and B1 ≤ B2 ≤ ... ≤ Bq, and 0 represents an empty sheet. Then for each number p received, if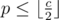 then we find an i such that Ai - 1 ≤ p and Ai > p (or Ai = 0) and put the number in the ith sheet. If
then we find an i such that Ai - 1 ≤ p and Ai > p (or Ai = 0) and put the number in the ith sheet. If 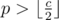 then we find a j such that Bj < p(or Bj = 0) and Bj + 1 ≥ p and put the number in Bj's sheet. As mentioned above in the editorial, the total round won't exceed
then we find a j such that Bj < p(or Bj = 0) and Bj + 1 ≥ p and put the number in Bj's sheet. As mentioned above in the editorial, the total round won't exceed 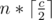 when we have filled all the sheets with a number (because each sheet won't be modified more than
when we have filled all the sheets with a number (because each sheet won't be modified more than 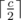 times), and as the two sequence are non-decreasing and all the numbers in the first sequence are smaller than all the numbers in the second sequence, we win the game.
times), and as the two sequence are non-decreasing and all the numbers in the first sequence are smaller than all the numbers in the second sequence, we win the game.
Checker in problem B is adaptive?
No, it isn't. That's explicitly stated in Russian version of the problem (but not in English one). Anyway hack format could give a hint for this.
Div 1.A two integers n and k (0 ≤ n ≤ 10^5, 1 ≤ k ≤ 10^18). ,but k is out of integers
K fits in a long long. Everywhere you have int (except for "int main"), replace it with long long.
"Integer" doesn't min "fits in
inttype".I got it... my English sucks
Auto comment: topic has been updated by ODT (previous revision, new revision, compare).
DIV2 D sample test case:why cant i write 2 on the second sheet then write 1 on the first sheet and win in 2 rounds?
Of course you can.If the second input is 3,you need 3 rounds too.
I was wondering the same thing....The problem statement is a little too big for me to grasp and understand...!
i now know the reason.
its because you have to make choice online,not after read all the numbers.
Ohh yess. You are right !
Div2E, the "Solution using map", why I'm not allowed to view the requested page
For DIV2 B.Chtholly's request, isn't the answer is ((k*(k+1))/2)*11?
No this is wrong.It makes your kth term 11*k which is obviusly only true uptil k=9.I dont think O(1) will exist as these numbers dont seem to form a mathematcal series.
Got it.Thanks
Can someone explain the Div 2E in more detail. I don't understand, how are equal numbers being created?
I got the how the equal intervals are being created. They are generated when we apply the operation 2.
In the code given in the editorial, the author has used
it_r = upper_bound(r + 1)instead ofit_r = upper_bound(r). Why?When I tried to click the"My solution"link of your div1E , codeforces told me that"You are not allowed to view the requested page" .Can you solve this problem? Thanks.
Solved.
In div2 E, I do not understand this step:
auto it_r(--A.upper_bound(r + 1)); if (it_r->first != r + 1) A[r + 1] = it_r->second, ++it_r;--A.upper_bound(x)find the last element that is ≤ x. Obviously, x is on that interval. Then divide the interval into [..., x - 1] and [x, ...] if x is not left endpoint.This step we want to divide the interval into [..., r] and [r + 1, ...], so use
--A.upper_bound(r + 1).That makes sense. Thanks man.
I'll have another take on Div1C. Why is the generator assumed to be random? (Or "sufficiently" random for this task?)
At least it can be easily proved that the period is long enough.
Could someone please provide the proof for the div1 C only taking m log n time? How do we know we only check an average of 1 interval each time?
For Div.1 C, std::vector is enough (we don't need a tree, or even std::set).
Suppose there are x intervals in the given range, and there are y intervals in total now. Then E(x) = y / 2 + O(1) if the intervals have the same length, since the given range is chosen randomly. I think E(x) = Θ(y) also satisfies when the input is random. So the time complexity of an operation using std::set = Θ(x) = Θ(y) = which using std::vector.
Surprisingly my submission 32877475 is one of the fastest now, though I think my std::vector operations are slow :)
Vector is enough in solving this problem, but I don't know how to prove its time complexity.
By the way, I think vector is harder to code than binary search tree...
Your code may get TL with this case:
100000 100000 833333337 1000000000Hmm, my solution with vector get TL, but this happened only because the random number generator is bad. All queries are of the first type. Is it possible to fail solutions with tree in the same way?
Hello everyone! I'd like to solve Div.2(A) in O(M log N), can someone give me a clue how to realize it with segment tree?
Did you predict that it would be problem G in the previous educational round?
hah, just luck, unfortunately, it this problem's solution was tutorialed here... many of us could get more rating for this round)
Div 2C / Div 1A is persistent treap))