Hi. I am trying to solve this problem.
For convenience, I have summarized the problem statement below (based on my understanding):
Given a directed graph with N vertices and E edges (with cycles and not necessarily connected), find the minimum number of edges that we need to retain such that connectivity between vertices is retained as given in the original graph.
Input size: 1 ≤ N, E ≤ 2e5
Time limit: 1s
For example, for the following graph:
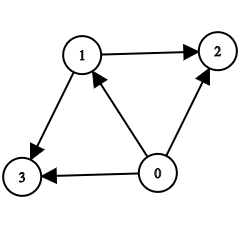
We should retain the edges:
0 -> 1
1 -> 2
1 -> 3
So we must use a minimum of 3 edges.
Note that:
0 -> 2 is redundant as we can use the path 0 -> 1 -> 2 to get from 0 to 2.
0 -> 3 is redundant as we can use the path 0 -> 1 -> 3 to get from 0 to 3. (Thanks filippos for catching this mistake!)
This problem seems to be asking for the transitive reduction of a graph which can only be found in at least O(n2) based on what I found on Google and this clearly wouldn't pass the time limit. Furthermore, the list of AC solutions suggests that there is a linear time solution to this problem.
Could someone please advise me on how to solve this problem?
UPD Managed to solve this problem (thank you please_delete_account for your incredible patience and explanation!).
I indeed had a wrong understanding of this problem and overly constrained it.
For readers who are looking for the solution to this problem, I have posted my solution below:











I think that answer to the given input should be
3instead of4as we don't need0 -> 3as we can use0 -> 1 -> 3:)Ah. You are right! Sorry for my slip-up. I have updated the sample.
I think you're trying to solve another problem than the one described in the link. You can build any graph you want as long as it satisfies the conditions. Your interpretation constrains the task and makes it a lot harder.
Think about line graphs and cycles, and about topological sorting.
I'm sorry but I couldn't catch your hint. Yeah. I think there must be some way to do it without finding transitive reduction. But I cannot visualize how to use topological sort for this problem.
Let's look at the connected components in our graph.
If a component is a DAG, then place the nodes in a line in the order of their topological sort. Otherwise place all the nodes in a cycle.