Всем привет.
17 декабря в 10:00 MSK состоится второй отборочный тур олимпиады. Больше информации можно узнать на сайте олимпиады.
Контест в тренировках: Отборочный этап Олимпиады Университета Иннополис. Второй тур. 2017-2018
2 декабря уже прошел Отборочный этап Олимпиады Университета Иннополис. Первый тур. 2017-2018. Тем, кто прошел в финальный этап по результатам первого тура, участвовать во втором туре не обязательно, но они могут это сделать, никак не повлияв на отбор. Призеры прошлых лет проходят в финал автоматически, зарегистрировавшись на соревнование. Также по результатам отборочных раундов пройдет отбор в Школу олимпиадной подготовки Университета Иннополис, информация по ней появится позже.
Спасибо тем, кто участвовал в первом отборочном туре, вас было много :). Это была одна из причин проблем с очередью тестирования. В этот раз мы постарались оптимизировать процесс и надеемся, что очереди не будет.
Предыдущие туры олимпиады можно найти по ссылке.
Задачи отборочного этапа готовили: dusja.ds, burakov28, julsa, KamilBek, josdas, budalnik, disa, lightning, VArtem, pashka, niyaznigmatul, FireZi, iilnar. Спасибо разработчикам PCMS за тестирующую систему, а также спасибо ilsaf13, который обеспечивает техническую поддержку олимпиады. Спасибо тем, кто прорешивал задачи: craborac, demon1999, haposiwe, zclimber, YakutovDmitriy.
После конца тура здесь можно будет обсудить решения задач.
Всем удачи!











Where can we find those who qualified from first round?
UPD: List of those qualified is here: https://olymp.innopolis.ru/ooui/innopolis-open-2017-2018/standings/all-final_en%20(1).html
Damn you were really close :)
zscoder, prepare your solutions beforehand, please.
For problem E, is there a deterministic approach? I used a probablistic one to try and find the best partition, but got only 50 points.
Yes, sure. The problem can be reduced to Knapsack-problem, and since the weights are small enough (linear on the input length), it can be solved in polynomial time. You still have to do several optimization (they are deterministic) to get full score.
Yes, I saw that with knapsack we can solve it in O(N2). What optimizations are you talking about?
Note that there are not many distinct weights. Also use bitsets to restore solution.
My solution works in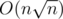 time (which might be a bit tight but it managed to pass on first try.) and
time (which might be a bit tight but it managed to pass on first try.) and 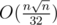 memory. Currently I'm not home so I don't have time to describe my entire solution but that should be my solution's complexity.
memory. Currently I'm not home so I don't have time to describe my entire solution but that should be my solution's complexity.
I see. The weights represent differences between pairs, and the sum of all values of all pairs is N, therefor there are at most distinct values. So we can do knapsack in
distinct values. So we can do knapsack in 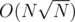 time, and in order to also maintain the actual sets we can use a bitset, which divides the memory by 32.
time, and in order to also maintain the actual sets we can use a bitset, which divides the memory by 32.
By the way, the best way to pick coefficients is by picking primes, the coefficient 1 and the pairs {1, 0}, {1, 1}? This is what I did and I think it's optimal but I'm not sure how to prove it. Edit: nevermind it's actually easy to prove.
Although there may be at most sqrt(n) different values, how do you update the dp with only O(1) each time for a value, even if that value has multiple occurrences?
Let dp[i][j] be the minimum number of type j numbers to get a sum of i assuming we use first j types. (-1 if impossible)
dp[i][j] = 0 if dp[i][j - 1] ≠ - 1.
dp[i][j] = dp[i][j - a[i]] + 1 if dp[i][j - a[i]] ≠ - 1 and dp[i][j - a[i]] + 1 ≤ cnt[j] (cnt[j] is the number of elements of type j we can use)
Note that you only need to store two rows of dp each time, so you can do this in O(N) memory. The state transitions are clearly O(1).
Also, to restore the answers, you can use a bitset for each type as "parent" array to backtrack and find solution.
Hi! How to solve a problem B for 100% ? I solved it only for 17% . Can you give a hint or an algorithm ?
You don't need to test every single value of i, there are only a few values of i that matter (I tested 10).
And how i can find a value of i ?
check a,b,c,d,1,n ± 1
Where can I find problems? Can I submit somewhere?
For the last elimination round, they created a gym with the problems from that round.
Here: Innopolis Open, Elimination round 2, 2017-2018
Full solution to C. Credits: niyaznigmatul, 300iq.
If n and m are odd, answer is -1.
If sum of array is negative, answer is -1.
Otherwise, we can always find an answer.
Take an arbibtrary cycle. For example, when m is even we can take:
Similarly, when n is even we can take:
Write down numbers in this order and compute prefix sums p1, p2, ..., pn * m. Let k be the index of minimal number among them.
Now, repeat this cycle infinitely many times and compute prefix sums on it again — p1, p2, ..., pn * m, pn * m + 1, ..., p2 * n * m, ....
You can notice that there is no pi < pk for any i > k. From this you can infer that pi - pk ≥ 0 for all i > k. This means that we can take a cyclic shift of this cycle and put k-th element in the end and this will be the correct answer (since there will not be such i that p'i < 0, where p' is a prefix sum array for this new cyclic shift).
Can somebody show me code of B?
Where the editorial?
I'm strugglig with problem D (Road Building), I keep getting WA 47. Could anyone tell me some corner cases or point out y mistake please?
deleted