Editorials of the first five problems in English will appear later.
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3856 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3462 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | -is-this-fft- | 162 |
| 3 | Dominater069 | 160 |
| 4 | Um_nik | 158 |
| 5 | atcoder_official | 157 |
| 6 | Qingyu | 156 |
| 7 | djm03178 | 151 |
| 7 | adamant | 151 |
| 9 | luogu_official | 150 |
| 10 | awoo | 147 |
| Name |
|---|



why problems A to C are Russian ?
because the problemsetters realized their mistakes in statements during the contest and now they are checking translation twice before publishing. be patient
okay :D
How to prove that the order of the selected guests is not important in 907E - Party ?
Sorry, I think the Russian version analyzes this fact and so the English will. This comment has no point.
We can think of it this way -- the problem can also be thought of this way.
Given a graph G = (V, E), what's the fewest number of vertices we can mark such that for every a and b in the graph G, there is a path between a and b such that all vertices on this path (except for possibly a and b) are marked.
This restatement makes it clear that the order of the guests is not important.
Could you show why this statement is equivalent?
Here is another way of thinking about it:
Consider two guests a,b with a being friends with b and x, while b is friends with a and y.
If a is processed first, then x and b will become friends, then when b is processed a and y, x and y will become friends.
If b is processed first, then a and y will become friends, then when a is processed b and x, x and y will become friends.
Either way the same endstate is reached.
Thus we can switch any adjacent guests without changing the endstate, so we can order the processing of the guests in any way we want (sort of like bubble sort) without changing the endstate.
"There are a couple of corner cases:" Goes onto listing 9 of them.
To be fair 6 and 7 can be combined by putting the segment with the even numbers first, but thats still 8 cases.
The images in 906E — Reverses are broken.
For 906E, what is the algorithm to split a string into a minimum number of palindromes (presumably in linear time, given the constraints)?
I've found a description of an algorithm for deciding whether a string can be written as a sequence of even palindromes (P*) here, but it doesn't seem like it could be easily extended to find the minimum number of such palindromes.
I've also just come across this paper from 2014, which gives a O(N log N) algorithm for finding the minimum number of palindromes in a decomposition — that still sounds too slow for N = 5 × 105.
O(N log N) too slow for N = 5 * 105?
Actually, I use the algorithm described in this paper. I have no idea why it is more than 20 times slower than one using the palindromic tree. It is also very unbelievable to me that solution with n = 106 can finish in 62ms.
solution with n = 106 can finish in 62ms.
To be honest, problem was changed few hours before the contest and I had not much time to prepare good testset. It is possible that bound on length of series isn't met in tests in such way that it lead the complexity to be
bound on length of series isn't met in tests in such way that it lead the complexity to be  in total.
in total.
You can check out my old entry on this topic.
Thanks, I'll give it a read when my brain is more awake — but it's still O(N log N) rather than linear. Is that fast enough for N = 5 × 105 (actually 106 since you interleave the two strings)?
Why would it be too slow? I think is just fine for n = 106 and 2s TL. And this solution also tends to have really good constant..
is just fine for n = 106 and 2s TL. And this solution also tends to have really good constant..
Also in practice the length of the serial links chain should be less than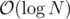 (I seriously don't know how to create a test for which to have a decent amount of chains with length approximately
(I seriously don't know how to create a test for which to have a decent amount of chains with length approximately 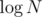 ).
).
Frequently O(N log N) isn't fast enough for problems with n = 106, but as you say, the constant factor is low. It probably also helps that the I/O is very cheap.
Can anyone help me to understand why is it possible to use random approach in div2E?
Good tutorial! But in problem div.1 D, I wonder why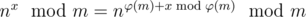 holds? Can anyone explain it a little bit? Thanks a lot!
holds? Can anyone explain it a little bit? Thanks a lot!
Here's a link that answers a similar problem. https://math.stackexchange.com/questions/653682/find-period-of-power-sequence-ak-mod-m-with-a-m-not-coprime/653696#653696
Well I don't consider these two problems similar... Maybe that's because I'm too stupid and know nothing about Maths. But I've carefully (maybe) read both the answer and the comments and failed to find a expression like this. So could anyone tell me how to get this by using the link above? Thanks a lot.
It's proven a bit in editorial. Remainders have period φ(m / a) if x > k, but if we will just take remainder of the division by φ(m / a) or by φ(m), we can get value that is less than k. To be sure that the power will be at least k, we add some number that is not less than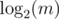 and is divisible by period length, and, obviously, φ(m) is such a number.
and is divisible by period length, and, obviously, φ(m) is such a number.
Understood! Thanks a lot!
Can you please tell me the proof why φ(x) is not less than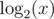 ?
?
For x = pk: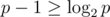
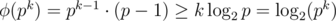
pk - 1 ≥ k, and
So
And for an arbitrary X function φ is multiplicative and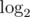 is additive, so inequality is obvious (except for x = 6)
is additive, so inequality is obvious (except for x = 6)
Thank you. That is a very nice proof.
I think in the tutorial to Problem 907A — Masha and Bears, the point 4-->(Masha likes last car, so it's size is not more than 2·V3) must be (Masha likes last car, so it's size is not more than 2·Vm) . @veschii_nevstrui
Yes, you are right, thanks a lot!
What am i doing wrong here for D?
Does anybody know any link for proof for statements made in 906D?
Why Probelm D has tag "chinese remainder theorem"?
I think it should be replace with “Euler Theorem”
can someone explain solution of div 2 C shockers problem in easy way??with use of set or without it also?? relpy fast pls
Consider a boolean value(valid) which becomes true whenever the size of set is 1 Case 1: '. w' Remove all the characters of the word w from the set Case 2: '! w' if(valid) increment shock
else retain all the elements in the set that are also in w Case 3: '? w' if(valid) increment shock else remove w from the set
For problem E, if we can reverse intersected substrings, is it an NPC problem or we can solve it in polynomial complexity?
Here's a randomized approach to 907D - Seating of Students that I think is easier to come up with than the editorial's & quite cleaner (although it is much less elegant):
Instead of dealing with a 2d grid, we can flatten out the grid. That is, instead of having the grid $$$[[3,2,4,5],[1,6,7,8]]$$$, we could have the grid $$$[3,2,4,5,1,6,7,8]$$$. Then, we know that something at position $$$i$$$ is adjacent to something at position $$$j$$$ iff $$$|i - j| = 1$$$ and neither $$$i$$$ nor $$$j$$$ is at the end (i.e. neither of them are $$$-1$$$ modulo $$$m$$$) OR if $$$|i - j| = m$$$.
We can incrementally build the grid. First, we take an arbitrary number and add it to a flattened grid. Say, we're building a $$$2 \times 4$$$ grid and our first number is $$$3$$$. Now, we can find out that $$$3$$$ can't be adjacent to adjacent to $$$1,4,5$$$ (using what we established in 1.) So once we chose our next arbitrary number, we have to make sure that the next number we chose can't be $$$1,4,5$$$. So if we do pick some of $$$1,4,5$$$, pick another number, and so forth, until you pick a valid number. Suppose we pick $$$6$$$. Now, we have a grid $$$[3,6]$$$. Pick another random number. If our new random number is either $$$1,4,5$$$ (since that's adjacent to $$$3$$$) or $$$4,5$$$ (since that's adjacent to $$$6$$$), then we re-pick until we get a valid number. In this way, we continue, until we have fully built our grid.
Just to formalize what's in $$$2.$$$ Suppose our incrementally build array is called
ans. To check if the last element ofansviolates any adjacency conditions, we just need to check two things (a)ans.size() % m != 1 % m && ans[ans.size() - 1] is not adjacent to ans[ans.size() - 2]. The first part is to account for the fact that just because two things are adjacent in the flattened grid, doesn't mean they're adjacent in the real grid (they usually are, but not when it's near the edge of the grid. (b)ans[ans.size() - 1] is not adjacent to ans[ans.size() - m - 1]. This basically accounts for vertical adjacencies.Anyways, for those interested, here's the code: 137380117. I'd be interested if someone could hack this, since I know randomized solutions are prone to hacking. Also interested if someone could say the probability of using the aforementioned procedure, but not getting a valid grid. It does happen on the 10th test case, so to remedy this, I just applied the procedure 1000 times and took any valid result. Not sure how often this happens, though.