How to solve this problem?
Consider a sequence s1, s2, ..., sn of n infinite binary strings (that is, consisting only of zeros and ones), where each character of each string is generated uniformly at random independently from others. Denote f(s1,s2,...,sn) = max LCP(si,sj), 1 ≤ i < j ≤ n where LCP is the maximum common prefix of two strings. Compute the expected value of f(s1, s2, . . . , sn).
Input
The only line of the input contains one integer n (2 ≤ n ≤ 10^4).
Output
Let the answer in the form of an irreducible fraction be P/Q. Then output P · Q^−1 mod (10^9 + 7).
Let's denote by Pk the probability that f(s1, ..., sn) ≥ k. Our answer is P1 + P2 + .... If 2k < n then surely Pk = 1. If 2k ≥ n then we have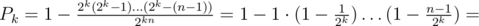
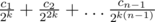for some coefficients c1, ..., cn - 1 that we can determine using simple DP. Summing these over appropriate values of k is easy.
EDIT: in fact that formula for P_k is the also for 2^k<=n, so there is no need to distinguish two cases here and we can make that summation from k=1 to infinity.