Straightforward implementation.
It leads to TLE if we implement the simulation step by step. Instead, we should directly compute the farthest position that we can reach for each given vector. Take care of some special cases, for instance, one dimension of the given vector is zero.
For each column, we can count the total number of different letters as cnt[i]. Then, by some simple observation, one can find that the answer is just 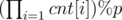 .
.
At first, we find out all the rows that have at least three consecutive “#”s. Note that only those rows with the minimum row index, second minimum row index, maximum row index and second maximum row index can in fact serve as the potential parallel sides of rectangles. Then, we deal with columns in a similar manner.
The following work is to enumerate all the feasible combinations of rows and columns so as to construct two rectangles (they may intersect or completely overlap with each other as the problem claims). Then, we compare each obtained board with the given one. If the given board contains two rectangles “correctly”, we will surely find out one single candidate result that is exactly the same as the given one. Otherwise, we can never find out any feasible answers.
Well, I find that this is a famous topic, referred to as Steiner Tree !! To solve this problem, one has to master several amazing techniques, such as dynamic programming based on bit-mask, SPFA (perhaps short for shortest path faster algorithm) and so on.
One can find a large number of materials talking about this topic on the internet, and even standard frameworks about how to write the codes (as far as I consider).









