yyjhzx's blog

Sum of GCD pairs in a given range of integers
By yyjhzx, history, 7 years ago, In English

Hi, i'm trying to solve the following problem : Given 1 ≤ m ≤ n ≤ 100000 , calculate:

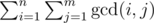
If n = m is kind of easy, but i can't think of anything for n > m.

PS:I think an 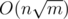solution or anything similar can be squeezed to pass TL , if you have any idea please share :D

  • Vote: I like it
  • +18
  • Vote: I do not like it

»
7 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

This can be done by phi function. kind of similar question good explanation link. If you understand that then this is pretty easy

→ Reply
  • »
    »
    7 years ago, # ^ |
    ← Rev. 2   Vote: I like it +1 Vote: I do not like it

    I don't see how they are related (with n != m), can you please elaborate? I already know how to solve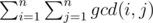 which is kind of the same as solving the LCM one..

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Can you Please give me the link of the question.I have an Idea.I want to check if it is right or wrong.

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        You can submit here.

        → Reply
        • »
          »
          »
          »
          »
          7 years ago, # ^ |
          ← Rev. 2   Vote: I like it +9 Vote: I do not like it

          If we calculate for n=4 and m=5 then your given expression(in this post) sums to 28.But In the problem link you gave me the answer should be 36.I don't think the problem is asking to find the above expression.

          → Reply
          • »
            »
            »
            »
            »
            »
            7 years ago, # ^ |
              Vote: I like it 0 Vote: I do not like it

            Still if you want to calculate the above expression i can tell you

            → Reply
          • »
            »
            »
            »
            »
            »
            7 years ago, # ^ |
            ← Rev. 2   Vote: I like it +1 Vote: I do not like it

            The problem is a variant.. It's easy to see that the problem asks for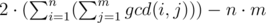 please read carefully, and the answer should be 28 for n = 4 and m = 5 , a simple brute-force can verify this.. Please share your ideas, any help is welcome.

            → Reply
            • »
              »
              »
              »
              »
              »
              »
              7 years ago, # ^ |
              ← Rev. 2   Vote: I like it +4 Vote: I do not like it

              Go through the link. Handwriting is pretty bad.If any doubt remains feel free to ask

              → Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it +18 Vote: I do not like it

dp[i] = number of pairs (a, b) that gcd(a, b) = i. It's very easy to calculate it in descending order: for i from min(n, m) to 1.

→ Reply
»
7 years ago, # |
  Vote: I like it +9 Vote: I do not like it

Apparently

You can precompute the values of ϕ in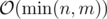 using a sieve and then compute the sum in 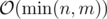, which should be fast enough.

I think you can use the technique from here to compute the sum in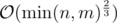 , similar to example two on the linked page, you just use the harmonic lemma for both n and m.

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Thanks for your reply, this is exactly what i'm looking for, but seems that i'm unable to prove :/ Any hints in how to prove this? Thanks anyway!

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it +13 Vote: I do not like it

      Turns out it's just a bunch of calculations. (Let's hope I didn't make to many typos.) If some step is hard to understand, you might want to look here for some simpler examples.

      → Reply