Hi Friends,
Greetings from CodeChef!
I would like to invite you to participate in the ACM-ICPC Kolkata-Kanpur Onsite Replay Contest and solve the same problem sets faced by contestants at the ACM-ICPC Kolkata-Kanpur Onsite Contest.
Contest Details: Time: 27th January 2018 00:00 hrs — 28th January 02:00 hrs Indian Standard Time — +5:30 GMT) — Check your timezone.
Contest link: https://www.codechef.com/KOL17ROL
Registration: You need to have a team and a CodeChef handle to participate. Team Registration Link: https://www.codechef.com/teams/register/KOL17ROL.
For all those who are interested and do not have a CodeChef handle, are requested to register in order to participate.
Good Luck! Hope to see you participating! Happy Programming !!
How to solve H and I ?
I — secrets of a person and his best friend are indistinguishable for this task, there are only 10! / 25 = 110000 states and Dijkstra works.
H — I have a very cumbersome square decomposition, nightmare to implement and I don't think it's supposed to fit in TL (but it does). For every value x that occur more than C times we store a segment tree (or you can use a treap instead) on a segment [0, A] (A is the values boundary). Queries we need to answer: number and sum of all numbers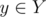
between l and r, where Y is the set (with repetitions) of y for every term |x - y|. To be able to update everything fast in these segment trees we do not count values y when y is a frequent number itself. Instead for pairs of frequent numbers we can make a square table a[i][j] = number of terms |xi - xj|. Now we can do all the updates in n / C, or 
.
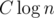How did you solve G?
In H I have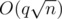
without any heavy data structures and it works about 1s on 1 random (though for my solution it is probably really maximal) maxtest and obviously gets TL. So I think that there are just no good tests against your solution.
Nice idea in I!
G: Let's iterate over all heights of the rectangle we want. For the moment let's also fix the y of lower side. Now the problem is 1D. For given left side there is maximal right side that we can afford, and this function is monotonous, so we can do two pointers. Now we don't fix the y of lower side. But still for every y we can do two pointers, therefore we can do two pointers overall (since we are interested in best variant over all ys). Each rectangle blocks a segment of ys, so we can maintain cost for given y in a segment tree. Complexity —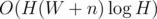
How to solve F? Also please add editorial:(
Can someone provide a working solution for problem H? Square root decomposition solutions are likely to timeout.