168A - Wizards and Demonstration
A straightforward mathematical problem, and it is better not to use any double numbers.
168B - Wizards and Minimal Spell
When we get a string starting with “#”, we should directly output it and go to the next line (in C++, it is “cout<<endl;”); otherwise, we output it while deleting all the space, and still stay at the current line (no “cout<<endl;”). We can adopt an “indicator” flag = 0, 1, which indicates whether the last input string starts with “#” or not (for instance, flag = 1 means yes). Note that when we meet a string starting with “#”, we should first implement “cout<<endl;” if flag = 1. Do not forget that when we meet the end of the input, we should implement an extra “cout<<endl;” if flag = 1.
168C - Wizards and Trolleybuses
First let us see what happens if the bus can keep accelerating until it reaches the terminal. It will have a speed equal to 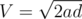 . Thus, for buses whose maximum speed vi ≥ V, it reaches the terminal with time
. Thus, for buses whose maximum speed vi ≥ V, it reaches the terminal with time 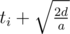 , where ti denotes the waiting time before departure. For the other buses with vi < V, it first reaches speed vi and then keep this speed until arriving at the terminal, which gives total time
, where ti denotes the waiting time before departure. For the other buses with vi < V, it first reaches speed vi and then keep this speed until arriving at the terminal, which gives total time 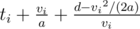 .
.
Next, when we are dealing with the i-th bus, if it reaches the terminal with longer time than the (i - 1)-th one, then it just arrives at the terminal with its “original” time; otherwise, it will catch up with the previous bus and reach the terminal with the same time.
Let us try to decompose the original problem into smaller ones step by step.
To win at least l tours, we should win l, or l + 1, or l + 2,..., or n tours. Thus, the total probability is the sum of probability to win exactly x tours (x = l, l + 1, ...n), and the original problem is reduced to computing the probability of winning exactly x tours. To win exactly x tours, we can win y (y = 0, 1, 2, ..., x) tours with prize (without bags) and x - y tours with bags (without prizes) while we should further guarantee that we have enough capacity to take back all the prizes. Thus, we have obtained two subproblems, and the first one is to calculate the probability of winning s tours with prizes and the second one is to compute the probability of winning t tours with bags while achieving a capacity c.
For the first subproblem, we can use dp1[i][j] to denote the probability of winning j tours among the first i tours, which can be calculated by pascal's triangle. For the second subproblem, we use dp2[i][j][k] to denote the probability of winning j tours among the first i tours while achieving capacity k, which can also be calculated based on pascal's triangle. Note that the maximum capacity can be vary large (about 200 × 200) and it is infeasible to compute all of them. Nevertheless, it is sufficient to compute for k up to 200. The reason is that there are at most 200 prizes and instead of calculating the probability of successfully taking all the prizes back, we can compute the probability that the prizes can not be taken back (therefore, 200 is enough for k) and then subtract this from the overall probability to obtain the result, like “set A and its complement set S - A” (S is the complete set). Therefore, we need a third dp3[i][j], denoting the probability of winning j tours among the first i tours (this is set S), which is also computed based on pascal's triangle.
Without loss of generality, we assume that a > b, and denote (a, b) as a state. The main framework is based on dfs. To check whether (a, b) is a winning state or a losing state, we can first test the result of (b, a%b). If (b, a%b) is a losing state, then it is obvious that we should directly implement a%b and thus leave the rival a losing state. If (b, a%b) is a winning state, then we must implement some a - bk so that after the rival implement several steps, he “has to take” us to the state (b, a%b), and thus we win. Now we focus on the analysis of the latter case, i.e., (b, a%b) is a winning state.
As a > b, we can write it as a = kb + r where k is the quotient and r is the remainder. One can check that if (b, a%b) is a winning state, then (a = b + r, b) is definitely a losing state, since either a - b or a%b directs to state (b, a%b). Based on this observation, we can further deduce that (a = 2b + r, b) is a winning state, as we can implement a - b and this directs the rival to a losing state (a = b + r, b). Similarly, we can determine the result of any state (a = kb + r, b), and in fact we have two general cases (for the following arguments, we might omit the second term b when we describe a state).
1) b is an odd number: the conclusion is that an odd k leads to a losing state while an even k results in a winning state, i.e., we have a state sequence “LWLWLW...”. We can prove this by induction. Base case k = 1 is obvious. Now we assume that this holds from k = 1 to k = n - 1. If k = n - 1 is an odd number, then k = n is an even number and must be a winning state since k = n directs to a losing state by implementing a - b. If k = n - 1 is an even number, as we are only allowed to implement a - bp and thus a - bp = nb + r - bp = (n - bp - 1)b + r. Note that bp - 1 is always an odd number and thus (n - bp - 1) is always an even number, which is a winning state. Therefore, we can only be directed to winning states, and thus k = n is a losing state.
2) b is an even number: the conclusion is that the state sequence has a period of length b + 1, and for every subsequence from k = n(b + 1) + 1 to k = n(b + 1) + b + 1, it has pattern as “LWLWLW...LWLWW”. More specifically, for n(b + 1) + t, t = 1, 2, ..., b, the state is winning if t is even; otherwise the state is losing and for t = b + 1, it is also a winning state. The proof is also based on induction. The base case is 0 × (b + 1) + 1, 0 × (b + 1) + 2,...,0 × (b + 1) + b + 1, and one can prove this after some simple deduction (0 × (b + 1) + b + 1 is a winning state as we can implement a - b2 = (b + 1)b + r - b2 = b + r and thus move to state (a = b + r, b) which is a losing state). Now, assume that the conclusion keeps true up to (n - 1)(b + 1) + b + 1, and we are going to prove n(b + 1) + t for t = 1, 2, ..., b, b + 1.
For any odd number t ≤ b, we can implement a - bp = (n(b + 1) + t)b + r - bp = (n(b + 1) + t - bp - 1)b + r, where p ≥ 1. Note that bp - 1 = (b + 1 - 1)p - 1 = q(b + 1) + ( - 1)p - 1 (binomial expansion), and thus a - bp = (n(b + 1) + t - q(b + 1) - ( - 1)p - 1)b + r. Here k' = (n - q)(b + 1) + t - ( - 1)p - 1, and one can see that n - q < n, and t - ( - 1)p - 1 is always an even number. According to our assumption, this is a winning state, and it implies that n(b + 1) + t is a losing state for odd t since we can only be directed to winning states.
For any even number t, it is straightforward that it is a winning state since we can move to t - 1, which is a losing state as proved above.
For t = b + 1, we can implement a - b2 = kb + r - b2 = (n(b + 1) + b + 1)b + r - b2 = (n(b + 1) + 1)b + r. Here k' = n(b + 1) + 1 and it is a losing state as we have proved and thus t = b + 1 is a winning state.









