ch_egor's blog

[Editorial] Codeforces Round #466 (Div. 2)
By ch_egor, 7 years ago, translation, In English
Tutorial is loading...

(Developing — vintage_Vlad_Makeev, ch_egor, V--o_o--V, demon1999)

Tutorial is loading...

(Developing — ch_egor)

Tutorial is loading...

(Developing — ch_egor)

Tutorial is loading...

(Developing — halin.george)

Tutorial is loading...

(Developing — Sehnsucht)

Tutorial is loading...

(Developing — cdkrot, ch_egor)

  • Vote: I like it
  • +56
  • Vote: I do not like it

Comments Comments (21)
| Write comment?
»
7 years ago, # |
  Vote: I like it +14 Vote: I do not like it

Thanks for the editorial !

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

For Problem F,cant we make p = sqrt(n) and get the complexity as n*root(n)?

Or did I misunderstood something?

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +10 Vote: I do not like it

    Complexity is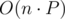 for movement of , and 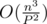for movement of . If you choose 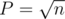you got .

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
      ← Rev. 2   Vote: I like it 0 Vote: I do not like it

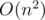      My bad

      Thanks for the reply

      → Reply
    • »
      »
      »
      7 years ago, # ^ |
      ← Rev. 3   Vote: I like it 0 Vote: I do not like it

      I'm having trouble understanding how those complexities are derived. Can you explain it in more detail? Thanks!

      Edit: figured it out.

      There are O(N^2/P^2) blocks, each with O(P^2/N) elements.

      Left pointer: For each block with O(P^2/N) elements, it takes O(P) to go from one element to the next. So the complexity for processing each block is O(P^3/N), and the complexity of processing every block is O(P^3/N) * O(N^2/P^2) = O(NP).

      Right pointer: For each of O(N^2/P^2) blocks, the right pointer moves O(N) times. The total number of times the right pointer moves is O(N^3/P^2).

      We can find the minimum complexity by setting the left and right pointers complexity equal. So NP = N^3/P^2, which gives P = N^(2/3). So the total complexity for both movements is O(N^(5/3)).

      → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

plz explain

n>=k part in problem c

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    extract prefix of length k and find the next string lexicographically.

    → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

In 5th problem it should be multiset and not set as there could be equal values.

→ Reply
»
7 years ago, # |
← Rev. 3   Vote: I like it 0 Vote: I do not like it

can someone tell me problem in this 35727835 __ __fixed now

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

The explanation for D kinda seems more complicated than it needs to be. I mean... the problem gives you three cases.

First case allows you to change a 1 to a 0 if some condition happens. Second case allows you to change a 0 to a 1 if some condition happens. Third case allows you to keep the current digit (with no condition).

Therefore, to solve, if the current digit was changed from a 1 to a 0, apply the restrictions for case 1; if it was changed from a 0 to a 1, apply restrictions for case 2. Else, no restrictions need to be applied.

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    All cases here are just for prove that we haven't other cases. It's obvious that we don't need upper bound for and lower bound for .

    → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

For multiset in E do we maintain a rolling sum. When inserting in multiset we add it to that sum and while removing ( if the size of multiset exceeds the required (i-j+1)/c elements ) we subtract. And final is sum of i-j+1 elements minus the rolling sum we maintained? Or we have to do something else?

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I don't get why you even need a rolling sum

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      'storing sum of minimums in some structure like std::multiset.'

      I did not understand this line in the editorial.

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
        ← Rev. 2   Vote: I like it 0 Vote: I do not like it

        So i also struggled with this line for some time. And here is what i figured:

        you'll need four things: a tree-multiset (multiset< int > ms), an integer containing sum (int sum), an integer with the greatest element in the multiset to be contained in the sum (the greatest summant; int geis) and an integer counting summants equal to geis in the sum (int nog).

        Firstly we set: ms = empty multiset, sum = geis = nog = 0; Only when ms.size() == c we reassign sum and geis with the first smallest number in ms: sum = geis = *(ms.begin()); nog = 1;

        Now, when you insert an element (int el) to ms you need to update sum and geis values only when ms.size() > c.

        1. If el < geis:
        sum += el;
sum -= geis; //we replace geis as a summant with el in sum.
if (nog == 1){
geis = *(ms.lower_bound(geis)--); // we find the first "old" geis position in ms and get value of previous element - this is our "new" greatest summant
nog = ms.count(geis);
} else {
nog--;
}
        1. If number of summants increase (ms.size() % c == 0) we add to the sum next value not less than geis:
        int geis_count = ms.count(geis);
if (geis_count > nog){
nog++;
} else {
nog = 1;
geis = *(ms.upper_bound(geis));
}
sum += geis;

        Please note, that each update requires O(1) searches (or other operations with the same complexity) in a tree-multiset of size O(n), thus requiring O(log n) time for each insert, O(n log n) time for each i in the main for loop and finally O(n**2 log n) for the solution.

        → Reply
»
7 years ago, # |
  Vote: I like it +5 Vote: I do not like it

For problem F: sorry, I don't understand why we should change t to one in O(1) time. And does it means that we should let r be the sequence of {r1, r1 + s, r1 + 2s, ...}(s = n2 / P2) and let l and t be different number in n as step of P so there may be O(n5 / 3 × n2 / 3) different movement.

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I think it's supposed to say that you can change t by one in O(1) time, i.e. go from t to t + 1 or t - 1 as necessary. What you do is sort the queries as described and answer them using Mo's Algorithm.

    → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

In editorial of F, how it's ensured after sorting that 1st type queries are calculated after the intended number of 2nd type queries for ex. lets say P = 10 so for number of change queries from 1 to 9 will fall together and there might be wrong ordering in processing them.

→ Reply
»
5 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Anyone have any idea why Problem D is tagged as Binary Search / Implementation? It seems more like a Greedy solution to me.

→ Reply
  • »
    »
    4 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    You can binary search for l and r. The idea is simple: just check if the conditions are satisfied at the points where we have "00001" or "11110" (because these are the ones which matter) for l and r separately (while doing the binary search). Since the answer is guaranteed to exist, you can find it by binary search too.

    → Reply