10 — 11 ноября прошел отборочный этап олимпиады "Волга-ИТ" в номинации "Алгоритмическое программирование".
Вот ссылка на олимпиаду: http://volga-it.org.
А вот ссылка на тур: http://vtcloud0.ulstu.ru/ru/contest-cid-138d-sh-1?ps=1&smt=1
Участникам предлагалось за 1,5 дня решить 13 задач. Влияло только количество решенных задач, штраф не учитывался. Мне довелось решить все задачи, поэтому проведу здесь разбор.
Задача А.
По условию в случае несбалансированности игры существует герой, способный победить любого другого героя в дуэли. Найдем кандидата на такого победителя.
Для этого пройдемся последовательно по массиву героев и будем на каждой итерации сравнивать текущего героя и лучшего на данный момент. Если текущий герой побеждает, то он занимает место лучшего. Заметим, что в этом случае все проигравшие уже точно не являются кандидатами на сильнейшего.
Осталось проверить нашего "лучшего". Для этого второй раз переберем всех героев и сравним кандидата с каждым. Если найдется герой, который не дает победить кандидату (помните о ничьей, где никто не побеждает), то игра сбалансирована, и мы выводим Yes. Иначе — No.
Задача B.
Для начала увеличим все получаемые очки в 2 раза, чтобы иметь дело лишь с целыми числами.
Посчитаем динамику dp[i][j] — вероятность набрать j очков за i игр. Ответ в таком случае — 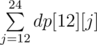 .
.
Переходы очень просты: dp[i][j] = dp[i - 1][j]·pLose + dp[i - 1][j - 1]·pDraw + dp[i - 1][j - 2]·pWin, где pLose, pDraw, pWin — вероятности проиграть, сыграть в ничью и выиграть соответственно.
Задача С.
Посмотрев на примеры, к тому же с рисунком, можно заметить, что если n·m — число перекрестков — четное, то каждый перекресток можно пройти лишь 1 раз. (точного доказательства, увы, не приведу). В этом случае в каждый перекресток входит ровно одна улица из маршрута, а значит ответ равен 20·n·m.
Если же количество перекрестков нечетное, то, как ни старайся, один перекресток придется пройти дважды (опять же, основано чисто на моей интуиции и на неспособности построить контрпример). В этом случае ответ — 20·(n·m + 1).
Задача D.
В этой задаче достаточно записать все цифры из запросов на соответствующие им места. Если после этого какая-то позиция в пароле осталась незаполненной, то ответ 0, иначе — выводим наш пароль.
Задача E.
Несложная в техническом плане, но достаточно неочевидная на первый взгляд задача.
Запишем задачу более формально:
Дана матрица a[][], найти количество различных линейных комбинаций ее строк по модулю 101. Заметим, что мы можем рассматривать лишь линейно независимые строки.
Каждая независимая строка может быть взята в ответ от 0 до 100 раз (на 101 раз ее вклад будет аналогичен 0). Всего таких строк count, значит полное количество их комбинаций равно 101count.
Как известно, count = rg(a). Ранг матрицы можно найти, например, с помощью алгоритма Гаусса за O(n2·m), что укладывалось в ограничения. Заметим, что искать ранг надо не в вещественных числах, а в целых по модулю 101.
Задача F.
Сначала решим задачу лишь для пути с первой стоянки на вторую.
Посчитаем динамику dp[i][j] — сколькими способами можно добраться из начального положения в клеткку (i, j). Так как двигаться можно лишь вправо и вниз, то dp[i][j] = dp[i - 1][j] + dp[i][j - 1].
Заметим, что количество способов добраться из (1, 1) в (n, m) равно количеству способов добраться из (n, m) в (1, 1). Пути "туда" и "обратно" независимы, поэтому ответ на задачу равен dp[n][m]·dp[n][m].
Задача G.
В этой задаче требовалось сделать ровно то, о чем говорилось в условии: перевернуть битовые записи чисел a и b, сложить полученные числа, перевернуть обратно сумму.
Задача H.
Отношения "i ненавидит j" задают нам ориентированный граф. Заметим, что если в этом графе есть цикл, даже вырожденный (есть ребра (i, j) и (j, i)), то способов рассадить детей нет.
Иначе для существования ответа требуется, чтобы максимальный путь в графе не превышал r. Максимальный путь можно было найти запуском "поиска в ширину" из каждой вершины, благо ограничения позволяли.
Также можно было провести топологическую сортировку графа. Пройдем по вершинам в порядке сортировки и посчитаем динамику 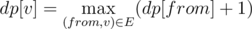 . В таком случае максимальный путь в графе —
. В таком случае максимальный путь в графе — 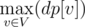 .
.
Задача I.
В этой задаче также необходимо сделать то, что требуется по условию — посчитать 2 средних геометрических N чисел. Так как N велико, то необходимо было для каждого числа x умножать ответ сразу на 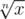 .
.
Задача J.
Подобная задача была на SNSS 2012 Round 1, только там надо было найти количество двоичных строк длины N, содержащих данную подстроку. Заметим, во-первых, что от размера алфавита ничего не зависит. Также очевидно, что ответ на нашу задачу = (26N - ans), где ans — ответ на задачу из SNSS.
Подробный разбор содержится в обсуждении того раунда: http://codeforces.net/blog/entry/4936#comment-100728.
Также на досуге можете почитать вот этот тред: http://www.cyberforum.ru/cpp-beginners/thread694502.html.
Задача K.
Отсортируем все отрезки по a[i], чтобы a[i] < a[i] + 1 или a[i] = a[i + 1] и b[i] > b[i + 1]. Теперь наша задача свелась к нахождению длины максимальной невозрастающей последовательности в массиве b. В самом деле, если b[i] ≥ b[i + 1], то это означает, что i + 1 отрезок вложен в i-ый по условию сортировки, что нам и требуется по задаче.
Решение этой задачи тоже недавно обсуждалось на КФ: http://codeforces.net/blog/entry/5541.
Задача L.
Так как N ≤ 1000, то возможно решение за O(N2): переберем возможную высоту буквы и возможную длину крайних горизонтальных линий, не забыв о проверке условия о длине средней черты. Каждая пара прибавляет к ответу (h + 3) / 2 - 3, где h — текущая высота буквы (деление целочисленное). Эту формулу можно получить, если внимательно посчитать количество доступных для рисования средней черты линий.
Задача M.
Заметим, что координаты xc и yc никак не связаны между собой и считаются аналогичным образом, поэтому достаточно научиться считать любую из них.
Будем хранить две переменные: sumX = xc·count и sumY = yc·count, где count — количество уже подвешенных грузиков. Зная sumX и sumY, мы быстро сможем находить xc = sumX / count и yc = sumY / count.
Разберем пересчет sumX: допустим, нам дан прямоугольник (x1, y1) — (x2, y2). Без потери общности будем считать, что x1 ≤ x2. В этом случае к sumX прибавится величина 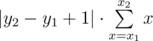 , так как в каждом столбце от y1 до y2 мы прибавляем одинаковую сумму по x.
, так как в каждом столбце от y1 до y2 мы прибавляем одинаковую сумму по x.
Для быстрого подсчета 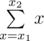 можно было использовать, например, префиксные суммы, посчитанные заранее: sum[i] = sum[i - 1] + i. В таком случае изменение приняло бы вид: |y2 - y1 + 1|·(sum[x2] - sum[x1 - 1]).
можно было использовать, например, префиксные суммы, посчитанные заранее: sum[i] = sum[i - 1] + i. В таком случае изменение приняло бы вид: |y2 - y1 + 1|·(sum[x2] - sum[x1 - 1]).
Аналогично пересчитываем sumY. Общее количество грузиков count увеличивается на |x2 - x1 + 1|·|y2 - y1 + 1|.











В I можно было найти среднее арифметическое логарифмов и взять exp от него. Вообще молодец, труд совершил.
Да, про логарифмы жаль, что не придумал)
В задаче В
проще сразу писать перебор.
В задаче С
очевидно, что если хотя бы одна сторона четная, есть такая раскладка:
В противном случае шахматная раскраска гарантирует, что хотя бы одна вершина будет посещена дважды. Мы можем использовать такую раскладку:
Где точку "?" мы первый раз проходим вниз, а второй — вверх.
В задаче F
Если не путаю, ответ
В задаче M
Первый раз вижу человека, который считает префиксными суммами сумму арифметической прогрессии с шагом 1. Если что,
Да, про арифметическую прогрессию мне уже сказали)
По M как минимум две попытки с декартовым деревом было :)
Хаха, кажется, я знаю, от кого)
А вообще по задаче М можно было вспомнить что такое центр масс. В частности тот факт, что возможно разделять все грузики на любые группы, считать центры массы этих групп и принимать это за целостный груз суммарной массы. Так мы и будем обрабатывать прямоугольниками, в качества центра масс будет их центр, в качестве массы — фактически площадь. Ну и по данной формуле в лоб за линейное время считаем уже для прямоугольников.
Я вот тоже не очень понял, зачем тут столько формул :)
Задачи оказываются все проще и проще, чем я думал)