202A - LLPS

It is sufficient to output all the letters with the maximum alphabet order. The reason is that if the optimal palindrome sequence has multiple different letters, we can simply delete all the other ones except for the maximum one, which gives a better result.

202B - Brand New Easy Problem

The solution is straightforward. We should consider all the n! permutation patterns and calculate the similarity.

202C - Clear Symmetry

Inspired by the tutorials, it suffices to only consider odd number n.

For odd number n, we divide the whole figure into several areas. Suppose that we draw a horizonal line crossing the m + 1-th row, where 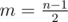, and another vertical line crossing the m + 1-th column. One can see that if there are a black squares in row r and column c, where 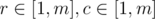, then there will be totally 4a black squares. If there are b₁ black squares in row m + 1 and columns 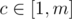, then there will be 2b₁ black sqaures in this row. Similarly, if there are b₂ black squares in column m + 1 and rows 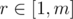, then there will be 2b₂ black sqaures in this column. Finally, there may be d = 0 or d = 1 black square in row m + 1 and column m + 1.

Next, we discuss based on the following two cases.

1) m is even: one can see that we can have any 4a + 2b₁ + 2b₂ + d black squares, where a = 0, 1, ..., m / 2, b₁, b₂ = 0, 1, ..., m / 2 and d = 0, 1;

2) m is odd: if d = 1, then for 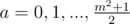, b₁, b₂ = 0, 1, ..., (m - 1) / 2, we can have any 4a + 2b₁ + 2b₂ + 1 black squares; if d = 0, then for 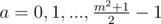, b₁, b₂ = 0, 1, ..., (m + 1) / 2, we can have any 4a + 2b₁ + 2b₂ + 0 black squares; for 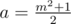, b₁, b₂ = 0, 1, ..., (m - 1) / 2, we can have any 4a + 2b₁ + 2b₂ + 0 black squares.

Finally, for the given x, we enumerate n from 1 until we find that there exists at least one solution for 4a + 2b₁ + 2b₂ + d = x according to the above cases.

202D - Guess That Car!

The trick lies in the formula c × d². Note that d² = x² + y², and thus dimension X and Y are independent if we consider x² and y² as an entity, which resembles Manhattan Distance. Thus, we can determine the optimal X and Y, respectively, and for simplicity, we only focus on how to calculate the optimal X (Y is similar).

First, for each column, we compute the sum of all the elements in different rows. Next, we enumerate each feasible position and calculate the cost and finally select the optimal one as position X.

202E - Fragile Bridges

The main idea is dp. For each node i, we use leftnoback[i] to denote the maximum points we can obtain if we start from node i and move to left but do not return back. In contrast, we use leftback[i] to denote the maximum points that we can obtain if we move to left but return back to node i (one can implement similar operations when moving to right, i.e., calculate rightnoback[i] and rightback[i]).

Then, we enumerate each position i again as the starting node, and we have the following feasible operations:

1) move to left and do not return to node i. This gives a value leftnoback[i];

2) move to left and return back to node i and move to right but can return or not to node i. This gives leftback[i] + max(rightnoback[i], rightback[i]);

3) move to right and do not return to node i. This gives a value rightnoback[i];

4) move to right and return back to node i and move to left and return back or not to node i. This gives rightback[i] + max(leftback[i], leftnoback[i]).

From all the above cases, we find out the globally maximum value.

Here are the details about how to compute leftback[i] and leftnoback[i] (note that this is similar for the “right” term).

We use x to denote the initial points between node i and its left node i - 1. If x = 1, then leftback[i] = 0 since we can never return back once we go to node i - 1. If x > 1, then leftback[i] = leftback[i - 1] + x / 2, where “/” is integer division. For leftnoback[i], we have leftnoback[i] = 1 + (x - 1) / 2 + max(leftback[i - 1], leftnoback[i - 1]).