WHERE IS IT?
Edit : Ok because of the delay we are unable to participate :/
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3856 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3462 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | -is-this-fft- | 162 |
| 3 | Dominater069 | 160 |
| 4 | Um_nik | 158 |
| 5 | atcoder_official | 157 |
| 6 | Qingyu | 155 |
| 7 | djm03178 | 152 |
| 7 | adamant | 152 |
| 9 | luogu_official | 150 |
| 10 | awoo | 147 |
| Name |
|---|



Where is it???
where is it??
You should check out this blog post:
http://codeforces.net/blog/entry/58674
April Fools?
We are in Moscow but we can't find the link too...
There is an onsite contest with the same problems (Moscode). I guess there was some trouble in the onsite contest.
https://official.contest.yandex.ru/opencupXVIII/contest/7895/enter : "The virtual contest is in progress. You are not allowed to participate"
Hi. How do you find this link? I couldn't find it at opencup.ru :(
I used
for i in `seq 7836 8000`; do wget "https://official.contest.yandex.ru/opencupXVIII/contest/$i/enter/"; done;in bash :/According to snarknews, the contest will start one hour later, at 12:00 Moscow time.
Do anybody want to join today in team ext64 with me and savinov ?
Sure, why not.
7 minutes and still no link ?
UPD: this one
https://official.contest.yandex.ru/opencupXVIII/contest/7895/enter now works.
Where is 2nd division link?
http://opentrains.snarknews.info/~ejudge/team.cgi?contest_id=10427
?
"Service not available"
http://opentrains.snarknews.info/~ejudge/team.cgi?contest_id=10387
What is this? Why it shows this link :D
This is previous year contest
how to solve B,H, E?
B: For each added point, consider all the points within the square with length equals to the twice of current answer and centered at this point. Try all the possible triples. There won’t be too many points.
H: dp[i][j]=min length of si - 1 when si=p[0..j]
H: dynamic programming:
dp[i][k]— what is the minimal length of sk - 1 such that there exists sk of length exactly i (it also should be a prefix of p). How to invent that state: think of brute force, understand that we should know lengths of sk, sk - 1 in order to generate sk + 1, then swap answer with one of dimensions (here I swapped the answer with |sk - 1|).Now recalculation is simple: if you have sk with a specific length and you know |sk - 1|, then you know minimal possible length of tk + 1, and you also know its maximal length (it's minimal value of z-function and |sk|; if you forget about the latter, you get WA 12).
I?
It can always be achieved with at most two operations [1, n], [1, n - 1].
So just check if it's possible to achieve in one operation. Otherwise, construct with the two intervals.
Can you explain how you do it in two operations?
You can deduce each element one by one.
For example, to make the sequence
10 4 3 5 7, the two constructed sequence should be7 2 1 2 7and3 2 2 3LOL. Thanks
D?
If there are no boundaries at 0 and L, you take n functions yi(x) = ai ± x, and position of k-th dog at time t, is k-th sorted value of all yi(t).
With boundaries answer is periodical over time with period 2L, so you should do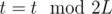 . Also you should add mirrored about the border lines and find k-th value in the interval [0, L]
. Also you should add mirrored about the border lines and find k-th value in the interval [0, L]
To find k - th value you can use binary search over answer, so you need to count number of yi < = checkValue, and that's possible to do with 2 binary searches over lines of same type.
That's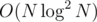
It's also possible to find k-th element of two merged arrays in O(logN) with few binary searches, instead of O(log2N).
k-th value of union of two sorted arrays A and B in O(logn):
Find the smallest
i : A[i] >= B[k-i-1]. Returnmax(A[i-1], B[k-i-1]).Proof. We want to take k smallest numbers = i numbers from A and k-i numbers from B. Then the k-th value is f(i) = max(A[i-1], B[k-i-1]). f(i) decreases until B[k-i-1] ≤ A[i] (i → i+1 means "change B[k-i-1] to A[i]").
How to solve C?
What is the expected solution for F ? I solved it with a general graph isomorphism algorithm.
Smart bruteforce + random?
Here I give a seemingly rigorous solution:
Suppose we can somehow identify vertices with value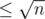 . The idea is that number of multiples for values in the range are distinct.
. The idea is that number of multiples for values in the range are distinct.
Vertices not adjacent to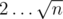 have value of prime number larger than
have value of prime number larger than  . Call this set of vertices S.
. Call this set of vertices S.
Then we can assign prime numbers greater than to S by its degree. e.g.:
to S by its degree. e.g.: 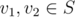 have same degree as the unknown vertices with value p1, p2, then we can arbitrarily give p1, p2 to v1, v2. Since somehow we cannot distinguish these 2 vertices.
have same degree as the unknown vertices with value p1, p2, then we can arbitrarily give p1, p2 to v1, v2. Since somehow we cannot distinguish these 2 vertices.
Now we identify all vertices with prime value. Hence we know prime factors each vertex has by its adjacent prime-valued vertices.
The next step is to identify vertices with power of prime value (pe). Simply group vertices with single prime factor and sort them by degree, the larger degree the smaller exponent.
For any other vertices, we can find exponents of its prime factors.
We tried the same, but failed to beat the TL. Can you share your code, please?
Here is the code. The backtrack function (and maybe other parts of the code) may still have some bugs that do not happen in this case.
How to solve A?
Concentrate on one player at a time, suppose the cards he ends up with are a1, ..., ak, with a1 being the best. Let bi be number of cards the previous player (the player who passes cards to the current player) has which are better than ai. Now process the cards of the current player from best to worst.
Card i either initially belonged to some starting hand out of which the previous player just drafted a better card (bi options) or it was the first card drafted from the starting hand of the current player (1 option). Exactly i - 1 of these options have already been taken away (by previously processed (better) cards of the current player), so bi + 1 - (i - 1) options remain, resulting in a total of ways to choose where the cards for the current player came from.
ways to choose where the cards for the current player came from.
The only thing left is to make sure that the current player started with at least one card, so we need to subtract the number of ways in which we never choose the second type of option, which is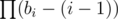 . The final answer is the product of the number of ways for each player. All this can be implemented in
. The final answer is the product of the number of ways for each player. All this can be implemented in 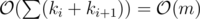 .
.