UPDATE: the editorial is here
Hello CodeForces! This year again, I'd like to invite you to the online mirror of an open championship of Switzerland called HC2 (the Helvetic Coding Contest). A mirror was also held last year and two years ago.

The Helvetic Coding Contest is a yearly contest held at the EPFL in Lausanne by the PolyProg association. The contest itself took place on March the 17th, but the online mirror is scheduled on Saturday, 14th of April, 10:05 Moscow time. The duration is 4:30.
Rules:
you can participate in teams or individually (1-3 people),
standard ACM-ICPC rules (no hacking),
the contest is not rated,
if you have participated in the onsite contest, please do not participate in the mirror.
The contest this year is Star Wars-themed. It features 6 series of 2-3 related tasks with increasing difficulty (easy/medium/hard). Sometimes it may be the case that a solution for the hard version solves all of them, but usually not. We think that the problemset is diverse and interesting, and while the contest is ACM-style, you will find that some problems are not so standard. Most easy&medium problems are even solvable in Python, so you can also recommend this contest to your newbie friends :) We promise to post a nice editorial as soon as the contest ends.
Acknowledgments: the problems were set by maksay, boba5551, mukel, DamianS, esrever, and myself. Thanks also go out to people who helped with the statements and testing: bgamlath, Michalina Pacholska (who also draws the cows), and KAN for CodeForces coordination, as well as everyone involved in the actual onsite contest, who are too many to name here. We also thank the sponsors Open Systems and AdNovum. Lastly, thanks to MikeMirzayanov for CodeForces and Polygon (which was used to prepare the problems).
Finally, in a bit of autopromotion, note that you can use Hightail to automatically test your solutions :) Good luck!
After-contest UPDATE:
>>> Editorial <<<
Feel free to ask questions in this topic.
Thanks to everyone who participated! We hope you have enjoyed the problems despite the interruption in judging. The top 4 teams, who have solved all problems, are:
SpicyFriedTomatoes: AbstractKangaroo, jqdai0815
(`・ω・´): King_George, ohweonfire, FizzyDavid
See you again next year!











hoping for short prob statements unlike previous year
what happens when onsite participator sees the problem with the help of other user ID.
That's why it's unrated
I think it's unrated because ACM style is always unrated instead. We do have contests that's rated that are later than their onsite contest.
I think u misread the dates .It's 17th of March (Not April).
Yes you are right. Sorry for this issue. It's my mistake. Thanks.
OH GOD, THIS PHOTO IS SO HOT
is it rated?
Why not :D
How to register as a team member...
I can't see it...
UPD: Fixed now, and wish everyone will enjoy the contest, GL & HF.
Thanks for noticing. It will be fixed as soon as possible.
And 3 hours later it hasn't be fixed still.Please be quick about it qwq
It's fixed now.
Thx a lot :)
there is no team option in the register form .
Why...the "register as team member" button doesn't show up.. Is that a BUG?
Why am I not able to register as a team?
It's now fixed!
If you want to participate in Helvetic Coding Contest 2018 in a team, but have already registered personally, just delete your personal registration on the page with a list of all registrations and register again.
I have a question. Why I can register as a team member?
Is It Rated?
Look this "Helvetic Coding Contest 2018 online mirror (teams allowed, unrated)".
Is it semirated?
Is it ln(2)-rated?
is it -1-rated?
Is it overrated?
FFS
I'm looking for a team to participate in the contest. Please PM me in case you want to solve it together :)
Can we register from two different teams ?
Someone want to take me on their team, or form a team?
Servers are down :(
5 queue pages
Will the contest be extended in that case?
I don't think so because it's unrated.
UPD : They extended for 30 min
Is scoreboard frozen??
Yes!!
contest extended by half an hour
We apologize for the technical problems with CodeForces. The queue is now moving again. The contest is extended by 30 minutes. It will remain unrated ;)
The editorial is up: editorial
We delayed the start of ARC/ABC by 10 minutes due to the extension of a contest in Codeforces. https://beta.atcoder.jp/post/220
I don't how to prove the correctness of the solution in the problem B2. Can you guys help me?
I didn't prove it during the contest, but here's a stab at it. Let g1, g2, g3, ..., gK be the vertices the prescribed solution adds, in order. Suppose you have a solution S which is better than the prescribed solution. Let p be the smallest integer for which gp is not included in S. Let the "cover" of S be all planets controlled by the rebels in solution S. Since gp is a leaf, it is not part of the cover of S. Let A be the nearest node in the cover of S to gp. If we rebuild S on vertex at a time, starting with g1, ..., gp - 1, then there is some first vertex B which when added to S causes A to become covered. Because of how gp was chosen, it must be at least as deep in the tree as B. Thus, we can remove B from S replace it with gp, without decreasing the score: we will gain all the planets on the path from A to gp, and at worst lose all the planets on the path from A to B.
Wow! Thank you very much. I really do learn something today!
Wow, this is proof is so wrong that I don't even know where to start.
If we rebuild S on vertex at a time, starting with g1, ..., gp - 1, then there is some first vertex B which when added to S causes A to become coveredSo you propose to remove $$$B$$$? If $$$B$$$ is among $$$g_1, g_2, g_3... g_{p-1}$$$, then does that not make your hypothesis invalid? And there is no reason why $$$B$$$ should be the $$$p^{th}$$$ element of $$$S$$$.
And even if we overlook this glaring error, you just show that if $$$g_p$$$ is the first such element, the score does not decrease. But it changes the graph completely. So it may happen that, in the long term, the set $$$S$$$ overcomes our proposed optimal algorithm.
By the way, I have a correct proof: it's main argument is cases on LCA of chosen points and infinite descent. So cool!
[del]
It does not say "1 <= ki <= n".
rly...
I made exactly the same mistake and wasted 40 minutes on it...
is there any O(Nk) solution of problem c2?
Great problemset today (especially B2, C3 and E2). Feel a bit sad for not figuring out B2 though...
I solved E3 with O(N2), not O(N2logN).
Our solution during on-site participation when we had little time left was to pick a random point of each type and check whether they line through them has an equal number of points of each type to the left of it. Repeat this until we finde a suitable line, then solve the subproblems recusively.
Is there an easy way of analysing the runtime?
Just did the virtual contest today, so I'm 4 weeks late to the party. Nonetheless I just wanted to get this out since I thought it was an interesting approach to an interesting question.
I claim that it's possible to find a dividing line that separates roughly into halves such that each half has equal spaceships and bases.
I'm not exactly sure how to prove it formally, so I will talk through it for even N and hope that the proof is largely correct.
Consider defining a half-plane by an angle theta from 0 to 2pi -- the dividing line is determined by the angle and theta and theta + pi are complementary half-planes. Moreover, we may shift the position of the dividing line so that N/2 points are on each side of the half plane.
Let f(theta) denote the number of bases contained in the half plane minus N/2. For general theta (theta such that no 2 points are parallel to the line), f is well defined and f(theta) + f(theta + pi) = 0, since the half-planes are complementary.
Note that f(theta) is "continuous" with respect to theta -- perturbing it slightly will include 1 more point and exclude 1 more point. Thus f will change no more than 1 at a time.
Thus, by "Intermediate Value Theorem", we have a point in which f(theta) = 0, which is the dividing line we sought.
To find this theta, we may binary search on theta by "Intermediate Value Theorem", starting from [0, pi] for example.
If we believe that our binary search will terminate in X steps, then this gives each dividing step a time complexity of O(NX), for a total time complexity of O(NX lg N).
(For this question X is not too large because the smallest gradient difference we can get is about 1/250^2. And by symmetry, a smallest possible angle between 2 lines lies between 0 and pi/4, so we can bound the smallest possible angle between 2 lines accordingly.)
Actually, there always is a line that separates both the spaceships and the bases into half (Proof: Consider the dual space, then the median-level of the bases and the median-level of the spaceships intersect an odd number of times. The primal of the intersection point gives us the line we're looking for.) Such a line is called a Ham-Sandwich Cut. It can be found in linear time, but the algorithms for it have quite large constants AFAIK. This would lead to an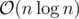 solution, but nobody would want to code something like that.
solution, but nobody would want to code something like that.
Very interesting. Thanks for the reference.
I had a different solution to C2 and C3, running in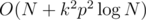 .
.
Let f(i, j) be the length of the smallest prefix which can be divided into i pieces with a total score of exactly j (or ∞ if there is no such prefix). The maximum possible score is k(p-1), so there are only O(k^2p) values to compute.
To compute f(i, j), consider all p possible scores for the last segment. Let this score be s. Then we can divide a solution into two parts: [0, a), where a ≥ f(i - 1, j - s) and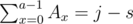 ; and [a, b), where b > a and
; and [a, b), where b > a and 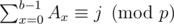 . Note that the final condition does not depend on a, so we may as well choose b = f(i — 1, j — s). Then we just need to find the smallest b greater than a with a given prefix sum (modulo p). For each remainder mod p we can precompute a list of all the prefix sums that have that remainder, and then binary search it in the inner loop.
. Note that the final condition does not depend on a, so we may as well choose b = f(i — 1, j — s). Then we just need to find the smallest b greater than a with a given prefix sum (modulo p). For each remainder mod p we can precompute a list of all the prefix sums that have that remainder, and then binary search it in the inner loop.
Thus, each of the O(k2p) DP states can be found in O(p) binary searches, for a runtime of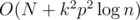 .
.
(Edit: fixed the formula)
How did people deal with overflow in F3? When multiplying two polynomials, the coefficients can be up to about 10082 * 105, which means you need to use a prime bigger than 232 in the number theoretic transform, which in turn means you have intermediate values bigger than 264 — and annoyingly Codeforces still uses 32-bit C++ compilers so no __int128.
I tried to get around it by using the convolution with two different primes and then using the CRT to reconstruct the value, but it was too slow. That could just be my FFT implementation, which I've often had time out on other problems.
Your formula doesn't display, so not sure what it says, but the modulo was only 1009, so at least standard FFT works well enough, with a maximum of like 200000 * 1009 * 1009.
I've fixed the formula. How do you determine the accuracy of standard FFT?
I managed to get a solution accepted using double-precision FFT, but only after I changed the range from [0, 1009) to [-504, 504] to reduce the size of the numbers. Without that I had WA (and long double got TLE).
Hmm, I myself don't understand the numerical stability of FFT too well. Experimentaly, all implementations that we had could handle 1009. With the neat trick you're describing, they could even handle 100009 AFAIR.
Actually I think that's a different trick. What we do to handle 100009 is to randomly set each number to either x or x-100009. Then it's in [-100009,100009], and half of the multiplied coefficients become negative, so that it cancels out to a way smaller number (around sqrt(n) times smaller, I guess).
I just multiplied using double FFT and added the result by 0.5 before rounding down. (Also, I used the trick to multiply using 2 calls to FFT instead of 3 making P[j] = A[j] + i * B[j] but that shouldn't matter). AFAIK, double works for things of value sqrt(10^9 + 7) because there's the trick of dividing a number v into v / B and v % B where B is around sqrt and using 4 multiplications to get the answer any modulo.
This also might help with precision http://codeforces.net/blog/entry/48465?#comment-325890 and the last problem here http://petr-mitrichev.blogspot.com/2015/04/this-week-in-competitive-programming.html is where I learned about this trick.
Yes, my precision problems are most likely from calculating powers of the primitive root incrementally.
Unfortunately Petr's blog only links to a comment in Russian, so I don't follow how the v/B and v%B trick works.
Divide the coefficients A[i] into 2 polynomials. A0[i] = A[i] % sq, A1[i] = A[i] / sq, so A[i] = A0[i] + A1[i] * sq. Do the same thing for the polynomial B. The answer is
C = A * B = A0 * B0 + sq * (A1 * B0 + A0 * B1) + sq * sq * (A1 * B1)
It works kinda like writing the numbers in base sqrt(mod)
Thanks, I follow. It does mean 4x as many FFTs though, which for my implementation would definitely push it over the time limit. Even my attempt at using two different primes plus the CRT only required 2x as many FFTs and that was too slow.
The FFT code here (method DOIT) is amazingly accurate (written by ko_osaga) http://codeforces.net/contest/958/submission/37318120
Actually, there's only need for 3x FFTs. One only needs to calculate A0*B0 , A1*B1 and (A0+A1)*(B0+B1) to get the answer. Also, more research about precision problems in FFT can be found in a research paper by matthew99 in Chinese.
Is there a faster algorithm than O(K2) for E2?
search up APIO 2007 Backup for O(nlogn)
There is a solution with lambda optimization.
Do you know any tutorial about this technique? This is the first time I have heard about it.
I think he means to refer to the IOI 2016 Aliens trick, you can read about it here: blog My submission 37355142 uses it for O(N·log(max)) complexity.
Another name is Lagrangean relaxation (if I understand correctly what you're referring to).
Let sort the given array and calculate differences between adjacent elements. Now we need to select k elements in array of differences, such that any two of them are not adjacent, and minimize their sum.
Let ignore the condition about k elements and maximize value of (sum — lambda * cnt), where cnt — number of chosen element ans lamda — some number. It can be done with O(n) complexity. It will be the best answer for cnt elements. The more lambda, the more cnt. We can make a binsearch and find such lambda when cnt = k. Answer to this lambda is answer to the task.
What about the proof that the function is concave?
Shame on the editorialist for problem B2. The proof is soooooooooooo hard. And all he writes is "exercise for the reader" and just describes the implementation. Yuck.