The Travelling Ant There is an Ant that lives in Baskerville and loves to travel. As Baskerville is a small place, it consists of only 5 cities placed one next to each other.
There is a train between each successive cities ie between City 1 — City 2, City 2 — City 3, ... City 5 — City 1. Note that our Ant loves to travel and gets happy after making exactly N train trips and returning back to home. Ant lives in the city 1 from where she begins her journey. She asks you to find the number of ways she can make N train trips and come back to home.
Since the number of ways can be huge, print that number modulo 10^9 + 7.
Input First line contains T, the number of test cases. Then T lines follow. Each line contains a single integer n, representing the number of train trips the ant needs to make.
Output For each test case, print a single line containing the answer to the problem.
Constraints 1 <= T <= 1000 0 <= n <= 10^18
Sample Input 3 0 3 4 Sample Output 1 0 6 Explanation In first case, ant has to make 0 trips. So the ant stays at city 1 and has only 1 option. In second case, ant has to make 3 trips. No matter what combination we try, we can never reach back to city 1 back after 3 trips. So answer is 0. In third case, ant makes 4 trips. There are 6 ways in which it can reach back to city 1. Way 1: 1-->2-->1-->2-->1 Way 2: 1-->2-->3-->2-->1 Way 3: 1-->5-->1-->5-->1 Way 4: 1-->5-->4-->5-->1 Way 5: 1-->5-->1-->2-->1 Way 6: 1-->2-->1-->5-->1
how can i solve this
Initially, it seems like you would need to use DP to solve this question, and while the solution I'm about to present technically could be considered DP, it really appeals to a more fundamental fact about matrices.
Take your adjacency matrix of the graph of cities, which we'll call A. It should look something like:
0 1 0 0 1
1 0 1 0 0
0 1 0 1 0
0 0 1 0 1
1 0 0 1 0
Now, if we calculate An, and call this matrix B, we notice that Bij gives us the number of walks from vertex i to vertex j of length n (to see why this is true, use induction). If you use fast power, you only need to do
matrix multiplications, and each multiplication will be on the order of 53 = 125, and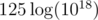 
should be well within any time limits.