I'm preparing for Team Selection Competition and these are some problems that I want to know how to solve. Problems are from previous competitions
Problem 1
Problem 2
Problem 3
Problem 4
| # | User | Rating |
|---|---|---|
| 1 | jiangly | 3898 |
| 2 | tourist | 3840 |
| 3 | orzdevinwang | 3706 |
| 4 | ksun48 | 3691 |
| 5 | jqdai0815 | 3682 |
| 6 | ecnerwala | 3525 |
| 7 | gamegame | 3477 |
| 8 | Benq | 3468 |
| 9 | Ormlis | 3381 |
| 10 | maroonrk | 3379 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 168 |
| 2 | -is-this-fft- | 165 |
| 3 | Dominater069 | 161 |
| 4 | atcoder_official | 160 |
| 4 | Um_nik | 160 |
| 6 | djm03178 | 157 |
| 7 | adamant | 153 |
| 8 | luogu_official | 151 |
| 9 | awoo | 149 |
| 10 | TheScrasse | 146 |
I'm preparing for Team Selection Competition and these are some problems that I want to know how to solve. Problems are from previous competitions
Given array with N < = 5 * 105 elements. Find number of subarrays such that every element in subarray appears even times
Given N < = 5000 strings. Find the number of pairs of strings such that after concatenating these strings, new string is palindrome
Given A, N, M . We perform this operation N times : A = (A+biggestDigit(A))%M . Find A after N operations. A < M < = 1018 and N < = 1018
Edit: biggestDigit(A) is digit with biggest value, not most significant one
Given N * N matrix A and Q < = 5 * 105 queries N < = 1000.
First query: 1 X Y, find farthest element in matrix such that its value is less than A[X][Y] (Manhattan distance)
Second query: 2 X Y VAL change element A[X][Y] to VAL
| Name |
|---|



Actually no! You can't consider it deterministic even in contest (here). Because such solution can easily be hacked using Gaussian Elimination. If you get experienced codes in your room they will hack you in no time :)
Probability of collision in Polynomial Hash is too low, something like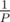 , but this xor hash has very high probability of collision. Actually the more numbers are there, more probability of collision you get.
, but this xor hash has very high probability of collision. Actually the more numbers are there, more probability of collision you get.
To be precise, if n > 64 then then it is always possible to generate a test case that breaks that solution, let alone n ≤ 105 :)
You can test yourself, run this code with the randomly generated array, it will find some cases where distinct numbers xor to 0 —
I think it's unfair to consider that the hacker has access to the randomly generated array — what if we generate the number with some high precision seed?
In CF you can see others' code, thus see the seed right? Use generator script to hack. :\
It is still hackable even if you seed with time. You can assume that CF will run your your hack between [T, T+10] seconds. You can just hack all of those seeds and create a test by concatenating them :)
Anyway, the point here is this xor hash can't be called deterministic. It is almost always hackable.
You can seed with micro/nano seconds which will cause some troubles to hackers tho :)
Even if you run it few times, what if you get different results? Which one are you going to take?
If you get even a single different result, then you skip that value (you can do something like a
map<pair<long long, long long>, int>and XOR every possible prefix)I have no idea why this is getting downvoted. The author asked for help, not a full solution. There is no point in spoiling the full solutions.
First task can be done with hashing.
First you need to make all numbers in range [1, N]. Than you can save binary string S with length N for each prefix of array : Si = 1 if we have odd amount of numbers i in current prefix, otherwise Si = 0. Now for current prefix and binary string S we add amount of same strings in smaller prefixes. This looks as O(n2) time complexity and memory (or even worse) — but we can use hashing. We can save hash values for all prefix strings instead of whole string and this will save our memory space. Also we should notice that string for prefix x and string for prefix x + 1 are different only at one position, so we do not need to hash whole string again, just need to change hash value for that position. Total complexity O(n).
Thank you Aleksa, I understood
1. It may be hard to solve if you've never seen the idea before.
First compress the array to [1, 5*10^5], after that imagine binary array of pairness of the compressed length for every prefix. For example if the array was [1 2 2 1], pairness array would be:
Now, string [si, si + 1, ...sj] is "good" for the task iff pariness arrays for prefix[i-1] and prefix[j] are equal. Now since those two arrays may be hard to compare for every [i, j], it would be good to hash them.
With generated hashes of those "binary strings" it should be easy to solve the task. Generating those hashes should take O(N(logN+F)), where F is for Hashing.
Thank you, I understood
Problem 2: The order of concatenation matters (for example, b and bc).
Note: this solution will calculate strings abc, and cba twice but will count abdkkmkk and dba once because of the order of concatenation. We can, however, avoid double counting if necessary.
Problem 4:
Note: we can add constant C to X - Y to avoid negative array indices.
For second problem, can we just compute hash value of string itself and its reverse and then check all N*N combinations (this must hold if new string is palindrome hsh1+hsh2*powerOfPrimeNeededHere = invhsh2+invhsh1*powerOfPrimeNeededHere)
I know I have asked for trie solution but just curious if hashing is going to work. By the way thank you, it will take some time to solve 4th problem
This problem is basically the same: https://www.codechef.com/problems/PP
Yes we can but it's O(N2). Sorry that I didn't notice the limits.