DonnieDarko's blog

How build a graph with points?
By DonnieDarko, history, 7 years ago, In English

If I want to build a graph when the input is a set of points
and an edge exists if the distance between two points is less than
some value x, what is the best way to construct the graph?

  • Vote: I like it
  • +15
  • Vote: I do not like it

»
7 years ago, # |
← Rev. 2   Vote: I like it +3 Vote: I do not like it

In the worst case the desired graph will have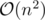 edges. So you might as well check distance between each pair of points and construct said graph in .

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +27 Vote: I do not like it

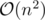    Thanks man! and in the case that I do not want to build the graph, but put each "component" in a subset, Is there a better approach?

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
      ← Rev. 2   Vote: I like it +8 Vote: I do not like it

      One (horrible) idea that comes to mind: put the points into square buckets of side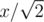 . The points within a bucket are clearly linked together. Compute the convex hull in each bucket. Then find the closest distance between the points of a bucket and those of its 12 relevant neighbors with rotating callipers. Link them if that distance is  ≤ x.

      → Reply
»
7 years ago, # |
  Vote: I like it +42 Vote: I do not like it

You could conpute the Delaunay triangulation of the points and then consider only edges which correspont to adjacent faces. This works because the Euclidean MST is known to be a subgraph in this (planar) triangulation graph.

→ Reply