I am getting tle in SPOJ GCDEX despite following 'A Dance with mobius function' blog. Please help.
My Solution: https://pastebin.com/TyQzd9Aw
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3856 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3462 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | -is-this-fft- | 162 |
| 3 | Dominater069 | 160 |
| 4 | Um_nik | 158 |
| 5 | atcoder_official | 157 |
| 6 | Qingyu | 156 |
| 7 | djm03178 | 151 |
| 7 | adamant | 151 |
| 9 | luogu_official | 150 |
| 10 | awoo | 147 |
I am getting tle in SPOJ GCDEX despite following 'A Dance with mobius function' blog. Please help.
My Solution: https://pastebin.com/TyQzd9Aw
| Name |
|---|



Auto comment: topic has been updated by JacobianDet (previous revision, new revision, compare).
I've noticed that your approach has complexity O(nlogn + sqrt(n)*T), I don't really know why exactly it still gives TLE even with some optimizations I made (even memoizing answers doesn't work), but I think there is an approach to get O(nlogn + T) complexity, maybe the upper bound for the value of sqrt(n)*T makes it hard to pass the strict Time Limit.
Your Solution with some optimizations (still TLE :( ):
https://pastebin.com/B2RKyUhV
My solution for the problem in O(nlogn + T):
https://pastebin.com/tC0CtDAJ
Thanks, this got AC. But why is the blog method not working.
Blog : https://www.quora.com/profile/Surya-Kiran/Posts/A-Dance-with-Mobius-Function
Well, I think it's because the post is from 2015 and the problem time limit was continuously updated, at the end of the statement it's announced that some AC solutions may get TLE after it.
Anyways, if the starting solution didn't pass the time limit, you'd need to improve any part of the algorithm that may cause it: In this case, the complexity per query might ruin the execution time so it's the first candidate.
My solutions preprocess each n and gets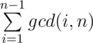 in a sieve style. After that just makes preffix sums to get the outer sum for each n and that would be the answer for each one.
in a sieve style. After that just makes preffix sums to get the outer sum for each n and that would be the answer for each one.
It just goes one step further that the blog's solution.
Thanks, I get that now