kayak's blog

Is builtinpopcount O(1) or O(log_2 k) ?
By kayak, 7 years ago, In English

In this comment, it's mentioned that the complexity of __builtin__popcount for any integer j with j = O(2N) is O(N) (i.e 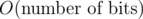) instead of O(1). So to count the number of one in a large binary string of length n with n >  > 64, if I split n into 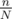substrings (with N = 64 / 32 / 16) and apply builtin popcount to each of the substrings and add them up, then the total time complexity should be 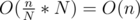instead of .

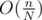But in page 101 of Competitive programmers handbook on the topic Counting Subgrids, based on the time taken to compute the results, the time should be same no matter if N = 64 for N = 32. But it turns out that they're different as "the bit optimized version only took 3.1 seconds with N = 32 (int numbers) and 1.7 seconds with N = 64 (long long numbers)".

Why N = 64 takes less time ?

  • Vote: I like it
  • +6
  • Vote: I do not like it

Comments Comments (9)
| Write comment?
»
7 years ago, # |
  Vote: I like it +5 Vote: I do not like it

The big O notation doesn't handle constants. Technically the complexity of __builtint_popcount is indeed the O(number of bits) but the constant is very small and much much smaller than a for loop checking each bit one by one although both have the same complexity, O(number of bits). So when you are using int numbers every for loop has to go twice the usual and a for loop has a larger constant than __builtin_popcount on a long long.

→ Reply
  • »
    »
    3 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    what do you mean by "the constant is very small"? I mean to say that if some func has complexity O(N) and the other has a for loop running for N times both can differ in constant? and what is the use of constant?

    → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Whatever the case of the complexity of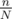 __builtin__popcount it does not surprise me that N = 64 is faster. Given that you are effectively calling the function times you would have twice as many function calls which can have some overhead which could be noticeable in huge tests like it seems to be the case with yours. It's important to note that your results could be slightly skewed depending on how you ran your testing — for example if you have run it singificantly large amount of times or not.

Also, depending on the compiler built in functions can have significant differences in performance

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I think it's inlined anyways so overhead is negligible.

    → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

It's because of a false data dependency that the compiler isn't aware of. There is no actual computational advantage of a 64-bit type, but because of how the compiler works it's less likely to hit this error when you use them.

https://stackoverflow.com/questions/25078285/replacing-a-32-bit-loop-count-variable-with-64-bit-introduces-crazy-performance

→ Reply
»
7 years ago, # |
  Vote: I like it +51 Vote: I do not like it

On modern hardware, there is a POPCNT processor instruction to count the number of set bits.

To utilize this instruction, the GCC compiler should be run with an option to enable the respective set of instructions. It is part of SSE4. Here is how to enable it from source:

#pragma GCC target ("sse4.2")
int s;
int main (void) {
	for (int i = 0; i < 1000000000; i++)
		s += __builtin_popcount (i);
	return 0;
}

In Codeforces custom test, I just checked with the GNU G++11 5.1.0 compiler.
With the #pragma, the code runs in under ~560ms.
Without it, the time increases to ~2370ms, which is four times slower.

→ Reply
  • »
    »
    4 years ago, # ^ |
    ← Rev. 3   Vote: I like it 0 Vote: I do not like it

    Gassa I saw another implementation of __builtin_popcount in this comment. Could you please tell me which one would be better to you? Are they essentially the same? Although running the popcount function using your test gives a worse runtime.

    → Reply
    • »
      »
      »
      4 years ago, # ^ |
        Vote: I like it +11 Vote: I do not like it

      If it was a bottleneck in a piece of code which runs for hours or days, I'd take various implementations (intrinsic, assembler, O(log log n), O(1) with precomputed tables), measure the time for each one in my particular use case, and settle on a winner.

      Incidentally, it's what I did back in 2007, which then resulted in the following piece of code — don't laugh, there was no popcnt instruction in my processor back then:

      res = (res & 0x55555555) + ((res >> 1) & (0x55555555));
res = (res & 0x33333333) + ((res >> 2) & (0x33333333));
res = ((res + (res >> 4)) & 0x0F0F0F0F);
res += (res >> 8) + (res >> 16) + (res >> 24);

      However, I expect the answer to vary between architectures and use cases. So, for a one-off program, such as a solution in the contest, I'd use the thing which is (1) easy to write and (2) usually not much slower than the other approaches. The __builtin_popcount intrinsic seems to be designed with these exact goals in mind — please correct me if I'm wrong!

      → Reply
      • »
        »
        »
        »
        4 years ago, # ^ |
        ← Rev. 2   Vote: I like it +10 Vote: I do not like it

        Thank you for your reply. I found this gcc bugzilla link earlier. The proposed implementation looks very similar to what you mentioned here!

        → Reply