Say we need to solve a recurrence of the form :
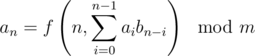
Here, f is an arbitrary function which can be computed in O(1). An example of such a problem is 553E - Kyoya and Train. The tutorial gives a solution in 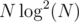 .
.
I recently saw a similar problem in codechef may long SERSUM, where I used another technique which I had thought of when I saw the prior problem. In this post I explain this very simple and intuitive sqrt decomposition solution, running in 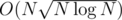 which works in almost the same time as
which works in almost the same time as 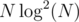 solution because of a very low constant. Here goes:
solution because of a very low constant. Here goes:
Let us divide into blocks of size say K, giving us a total of ⌈ N / K⌉ blocks. Block t consists of [(t - 1)K, tK - 1]
Let 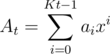 .
.
Let Ct = AtB.
When processing the block t + 1 we assume that we know Ct, which is computed when block t has been completely processed. So, we compute Ct a total of 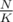 times using FFT in time
times using FFT in time 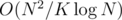 .
.
Consider some n between [tK, (t + 1)K - 1]. Then, 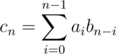
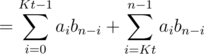
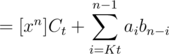 .
.
Clearly, the right part can be calculated in O(K), and we have an extra time of O(NK) because of this part.
Overall complexity = 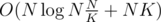 , which is minimized taking
, which is minimized taking 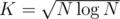 , and overall complexity is
, and overall complexity is 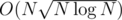 .
.
An optimization:
Note that the right part can be computed with only one mod operation if we use m2 = m * m, and keep subtracting m2 when the total sum exceeds it. Eventually we take total sum modulo m. This is a very common technique, which we use in matrix multiplication as well.
This means that we should use a block size even greater than 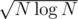 for better results, because of a huge constant difference in the two parts. (Computing Ct using FFT, and computing the remaining sum in O(k) using brute force iteration with the optimization above.) Just as an example, for N = 105, and m = 109 + 7 (which is a bad mod value for FFT problems), the best performance comes when you take K ≈ 6 × 103. For this input size it runs in about 2 seconds, which is pretty good.
for better results, because of a huge constant difference in the two parts. (Computing Ct using FFT, and computing the remaining sum in O(k) using brute force iteration with the optimization above.) Just as an example, for N = 105, and m = 109 + 7 (which is a bad mod value for FFT problems), the best performance comes when you take K ≈ 6 × 103. For this input size it runs in about 2 seconds, which is pretty good.










Hmm. So it still needs FFT? The main benefit I'd expect from sqrt decomposition here would be eliminating the need for FFT, so that's too bad. For smaller convolutions, FFT can be replaced by Karatsuba (worse complexity, handles arbitrary mod, can have a better constant), but that doesn't seem to be the case here.
With m = 109 + 7, how do you use FFT? AFAIK, the modulo is bad because there's no fast NTT for it (m - 1 is only divisible by 2 once). Do you use doubles? Or does modulo affect the speed of your FFT?
You can compute the convolution with an arbitrary modulo using normal FFT. It is described in On Fast Fourier Transform.
That's why I asked "do you use doubles?". That's what normal FFT means to me.
Yeah, it still needs FFT. I just wanted to share a more intuitive approach compared to the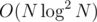 one. That one is also pretty simple to understand and implement once you see the solution, but not as intuitive (for me, atleast).
one. That one is also pretty simple to understand and implement once you see the solution, but not as intuitive (for me, atleast).
I use doubles for FFT (breaking the polynomial coefficients into x = y * sqrt(MOD) + z) to reduce the input coefficients increasing precision. You can see my implementation here. It uses 4 FFTs to find precise polynomial multiplication.
Mm, I agree that it's an interesting concept, I just don't see it having much contest use at the "I know when to use what FT" level — the D&C approach is simple enough and fast enough when written properly (I have 1.5 seconds on a typical online judge with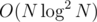 and a good modulo).
and a good modulo).
Being able to skip FT or at least working without doubles for arbitrary modulo, on the other hand (Karatsuba), are the kind of advantages that make something a practical alternative to FFT.
If we use Karatsuba and the D&C approach it will probably be comparable to the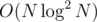 (especially when the modulo isn't NTT friendly and you would spend additional convolutions), given that Karatsuba will maintain its complexity:
(especially when the modulo isn't NTT friendly and you would spend additional convolutions), given that Karatsuba will maintain its complexity: 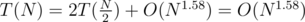 .
.
Auto comment: topic has been updated by jtnydv25 (previous revision, new revision, compare).