gaucho_josecito's blog

Find number given two remainders
By gaucho_josecito, history, 7 years ago, In English

Hi.

So I took part in yesterday's contest and I realized that for problem E, instead of considering the ball bouncing on the walls, we can just imagine there are infinite rectangles on the plane, one next to the other, and the ball will continue forever in the initial direction. We need to find if at any given time, x will be a multiple of n and y will be a multiple of m. This problem is analogous to the original one.

So we need to find a number k such that n|(x + vx * k) and m|(y + vy * k). This is similar to "find the first number that satisfies a given remainder modulo n and a given remainder modulo m". That's where I got stuck. I thought about Chinese Remainder Theorem, but since numbers are not necessarily coprime, it wouldn't work. I also thought about something in the terms of Euclidean algorithm, but I couldn't come up with anything either.

So, how can I solve that problem: find the first number that satisfies a given a remainder modulo n and a given remainder modulo m.

Thanks in advance!

  • Vote: I like it
  • +29
  • Vote: I do not like it

»
7 years ago, # |
  Vote: I like it +15 Vote: I do not like it

I use the same idea to solve this problem. You need to find numbers p and q such that

p * n = x + vx * k (1)

q * m = y + vy * k (2)

(1) * vy — (2) * vx:

p * n * vy — q * m * vx = x * vy — y * vx

You can rewrite this as a * p + b * q = c, where a = n * vy, b = -m * vx, c = x * vy — y * vx.

It is Diophantine equation. So, if c mod gcd(abs(a), abs(b)) != 0 then answer is -1. Otherwise, you can find all solutions of this equation. For each solution k = (p * n — x) / vx. You need to find positive k with the minimal absolute value.

You can see my solution here.

Sorry for my bad English)

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

This document explains it..

→ Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

If you have system

You can substitute it by equivalent system

System has a solution iff .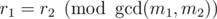

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +5 Vote: I do not like it

    Yeah but the new modules may still be non-coprime. E.g. m1 = 23·3·5, m2 = 2·3·53 gives new modules 22, 2·3·5, 52. Probably using gcd or lcm you can factor modules into coprime components..

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it +5 Vote: I do not like it

      Oh, damn, I believed that is the correct way for several years :(

      → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Also it's not equivalent system, because e.g. for the example above you maintain requirement only for 22 whereas the original system has requirement for 23. (You can see also that the LCMs are different).

    → Reply
»
7 years ago, # |
← Rev. 3   Vote: I like it 0 Vote: I do not like it

I have looked how it's implemented in Sage. Assume we want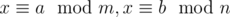 . Using Extented Euclid algorithm you compute α, β such that:

α m + β n = gcd(m, n).

Note that

Then you "lift" the solution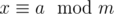 by a particular multiple of α m (it is congruent to 0 mod m and congruent to gcd(m, n) mod n):

Here, if (b - a) is not divisible by gcd(m, n), then there are no solutions.

→ Reply
»
7 years ago, # |
  Vote: I like it +10 Vote: I do not like it

I would like to note that many implementations work with numbers near to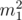 or even 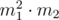which can be greater than 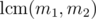. So I'll share our implementation.

→ Reply