Temirulan's blog

How to solve this magic problem?
By Temirulan, history, 7 years ago, In English

Given two weighted trees. f(x, y) — distance between x and y in the first tree, g(x, y) — distance between x and y in the second tree. How many pairs (x, y) such that x < y and f(x, y) < g(x, y). Number of vertices <= 2*10^5.

  • Vote: I like it
  • +61
  • Vote: I do not like it

Comments Comments (24)
| Write comment?
»
7 years ago, # |
← Rev. 2   Vote: I like it +11 Vote: I do not like it

I think my thoughts can help.

Let s1[v] be the sum of distances from first tree root to vertex v, similarly s2[v] the sum in second tree

s1[x] + s1[y] - 2 * s1[lca1(x, y)] < s2[x] + s2[y] - 2 * s2[lca2(x, y)]

then s1[x] - s2[x] - 2 * s1[lca1(x, y)] < s2[y] - s1[y] - 2 * s2[lca2(x, y)]

let a[v] = s1[x] - s2[x] and b[v] = s2[y] - s1[y]

a[x] - b[y] < 2 * s1[lca1(x, y)] - 2 * s2[lca2(x, y)]

I'm sure that is the correct way to solution

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +5 Vote: I do not like it

    Shouldn't the first equation and following contain

    2s1[lca1(x, y)]

    and

    2s2[lca2(x, y)]
    → Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it -29 Vote: I do not like it

You're looking for number of paths of positive value in weighted tree with weights g-f. Then you can do centroid decomposition or whatever.

EDIT: ah, sorry, I don't know why, but I assumed trees have same shape and differ just by weights. Ignore my post

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +38 Vote: I do not like it

    "Given two weighted trees." What are you talking about?

    → Reply
»
7 years ago, # |
← Rev. 4   Vote: I like it 0 Vote: I do not like it

One observation: we are actually looking for the number of pairs (x, y) such that f(x, y) = g(x, y).

UPD NVM is wrong.

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    why?

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
      ← Rev. 2   Vote: I like it -10 Vote: I do not like it

      The answer is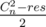 where res is the number of pairs (x, y) such that f(x, y) = g(x, y).

      UPD NVM is wrong.

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Wut?

        Consider N = 2. 1st tree is an edge with weight 10000. 2nd tree is an edge of weight 1. Are you telling that the answer is 1?

        → Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it +18 Vote: I do not like it

Remark: This problem is similar to the one analyzed in this blog. You probably won't understand anything below unless you read it before.

Let's fix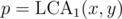 , then we have to find the number of pairs such that 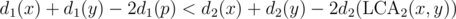. If we make a new tree T2' such that for every node v in T2, there is an edge (v, v') with weight d1(p) - d1(v), we have reduced our problem to finding the number of vertices that are within a distance D > 0 of each other.

However, the problem with this solution is that it would work in O(N2) if T1 was a path.

We can use the technique of "centroid decomposition on edges" and auxiliary trees to speed it up to . If h(x) is the distance to the active edge while doing centroid decomposition, we have to find the number of pairs such that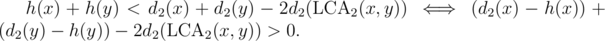

If we attach an edge (v, v') with weight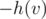 for all v to our auxiliary tree (which contains the vertices of tree 2 that we're currently processing), we have once again reduced the problem to finding the number of positive-length paths.

Total complexity: .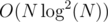

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    "Let's fix p = LCA1(x, y) and never deal with that" is not a good way to solve a problem.

    I didn't understand anything but I also cannot understand anything in the previous article.

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      This solution is identical to bciobanu's. Can you point out the parts you don't understand? I am genuinely not sure why the relevant parts in the first article (i.e. "And finally [...] and so on." and "Let's start by [...] O(|A|) nodes") are completely unintelligible. Unfortunately, I do not know of any English-language articles that talk about the concept of "auxiliary" trees. However, you can read the code for it here: https://blog.sengxian.com/algorithms/virtual-tree.

      → Reply
»
7 years ago, # |
  Vote: I like it +33 Vote: I do not like it

Here's an idea in .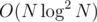

First suppose the second tree is a line tree. Let's relabel the nodes according to it, so that the edges will be 1-2 2-3 3-4 .. N-1 - N.

We'll divide and conquer over this line; for a fixed M we want to count the number of pairs x ≤ M < y which satisfy f(x, y) < g(x, y). We have that g(x, y) = g(x, M) + g(M, y). Root the first tree in an arbitrary node; we will make the following notation: f(x) = f(x, root).

Re-writing the condition: f(x) + f(y) - 2 * f(lca(x, y)) < g(x, M) + g(y, M). Let v(x) = f(x) - g(x, M). We'll re-write again: v(x) < 2 * f(lca(x, y)) - v(y).

To follow-up with an alright complexity here, only some nodes of the divide-conquer from the second tree will be active at some step. We'll build the virtual tree (i'm not sure if this is how it's called in the folklore, here is one problem which mentions it in the editorial, perhaps you could go from there) consisting of these nodes in the other tree. Counting the number of good pairs can be done with a min-max-merge on this tree we've built.

Now, before we move on to arbitrary trees, note that we've used the fact that M splits the active nodes in only 2 sets. If it were to split it K sets, like a normal centroid decomposition would, we would have an additional in time complexity, because when we query how many v(x)'s are less than a given value, we would also have to keep track of K colors, not only 2.

Following up on arbitrary trees, we'll binarize the second tree while maintaining distances. To do this, we can root it in an arbitrary node and convert any adjacency list of length greater than 2 similar to a segment tree construction. This way, we preserve distances, while adding only O(N) dummy nodes.

→ Reply
  • »
    »
    7 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    Can you explain how do you find the number of good pairs in the virtual tree fast? Won't you need another inner centroid decomposition, but this time on the compressed/Virtual tree?

    UPD: Nvm it can be easily done with DSU on tree and segment tree.

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it +10 Vote: I do not like it

      Yeah, i was thinking the same, but on a second thought, i didn't quite get the complexity right.. this way we'll do .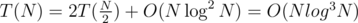

      However.. if we use sqrt buckets (keep the array sorted along with a buffer of at most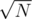 elements) instead of ST for the DSU, we'd get .

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
        ← Rev. 2   Vote: I like it 0 Vote: I do not like it

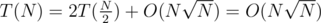        You can reduce it to finding the number of positive-length paths by attaching a leaf v' to each vertex v, where the edge (v, v') has a weight of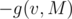 , which is solvable by a simple centroid decomposition. (Our solutions only differ in that part, by the way)

        → Reply
        • »
          »
          »
          »
          »
          7 years ago, # ^ |
            Vote: I like it +5 Vote: I do not like it

          Well this was the inner centroid decomposition I was talking about. Unfortunately it's again .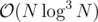

          → Reply
          • »
            »
            »
            »
            »
            »
            7 years ago, # ^ |
              Vote: I like it 0 Vote: I do not like it

            You're right, it is actually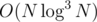 but it may be possible to speed it up by using a faster integer sorting algorithm.

            Let dc be the array of distances from centroid c to every one of its children. Also, let d'u be the elements of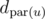 that are in u's subtree. We have therefore reduced this problem to counting the number of pairs in an array with positive sum. Obviously, this runs in O(n + S(n)), where S(n) is the time required to sort n elements. I think it may be possible to cheat here by using a fast integer sorting algorithm.

            → Reply
            • »
              »
              »
              »
              »
              »
              »
              7 years ago, # ^ |
                Vote: I like it +10 Vote: I do not like it

              As a last resort =)), binarize the virtual tree as well and when doing centroid decomposition, recurse first, and along with the result, get the values from the subtrees in sorted order and merge them in O(N). This probably fixes the time complexity back to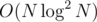 , but it's a headache.

              → Reply
        • »
          »
          »
          »
          »
          7 years ago, # ^ |
            Vote: I like it +18 Vote: I do not like it

          I feel like for an adequate book-keeping in a centroid step on the virtual tree we'll need some form of sorting.

          → Reply
          • »
            »
            »
            »
            »
            »
            7 years ago, # ^ |
              Vote: I like it 0 Vote: I do not like it

            It simply converts to number of paths of length  ≤ K which cannot be solved faster than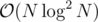 with centroid decomposition.

            → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        I'm not sure I got the sqrt decomposition way. Can you please explain it in some more details.

        Btw the trick of using SQRT decomposition in such divide and conquers to reduce the complexity is really nice. Thanks for sharing it!

        → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +10 Vote: I do not like it

    Following up on the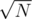 , we need a data structure to perform:

    1. insert(value)
    2. query(K) = number of elements  ≤ K

    We'll keep two arrays, namely A and B. Whenever we insert a value, we'll push it to the back of B. If B's capacity exceeds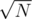 , sort it, and then merge it with the elements from A in 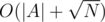. For N inserts, its amortized complexity is .

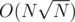    For a query, do binary search on A and brute search on B. It's .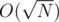

    Now, when combining it with DSU: T(N) = T(N - A) + T(A) + ??. Now, you'd normally replace ?? with min(N - A, A). But it our case it's not convenient. If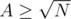 , then we'll merge the structures in O(N).

    If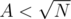 we'll push them regularly on to B and if it exceeds, we do what we did above. This all amortizes to .

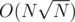    I guess there are some other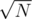 paths we could have chosen here. Another quick one would be keeping 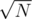lists inside each DSU, the i-th list representing the elements from 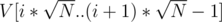, where V is the sorted array with all costs. On a query we take the lists by hand and brute-force the current query element's list.

    → Reply