ovis96's blog

What is the minimum distance Runu needs to walk?
By ovis96, history, 6 years ago, In English

Given n circles in 2D coordinate system (their centers and radius, circles can overlap). You are also given the position of Runu. What is the minimum distance she needs to walk to get out of all the circles. More formally, if Runu's position is P and there is a point Q such that Q is out of every n circles, you have to minimize the euclidian distance of P and Q for all such Q's .

This problem is out of judges, came to my mind. Can you provide me a solution? What is the tight bound of n then? If anyone had seen problem like this before or thought something like this, please do share.

  • Vote: I like it
  • -18
  • Vote: I do not like it

»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Auto comment: topic has been updated by ovis96 (previous revision, new revision, compare).

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

I don't really get the last sentence of the first paragraph, do you want to find the closest Q to a given P? If so then I believe that the following works. You binary search on answer, decrease radii of all circles by that number and check if P is covered by any circle.

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    No. For every R you can cover a circle of radius R with center in P with circles of radius 1. This implies that the answer can be arbitrarily large even if all radii of circles are equal to 1.

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Fair point. Well, I was firstly mistaken when thinking that building a circle of radius r from center P and checking if there exists some non-covered point is the same as the solution I described and secondly for binary search to be even appliable in this manner.

      → Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Thanks for commenting! You get the problem right. But binary search on answer does not work in some cases like ->

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Yeah, I admitted that in my second comment already, got that case myself)

      → Reply
»
6 years ago, # |
← Rev. 2   Vote: I like it +16 Vote: I do not like it

Kinda standard solution in O(n^2 log n): it can be proven that the answer is minimum such R that there is a point on border of one of the circles such that it is not covered by any other circles and it is on distance R from P. For every two circles find which arcs of each other borders they cover (this is simply circle intersection algorithm). After that, we need to find uncovered parts on each border in (almost the same as finding the union of several segments on line, but on circle in this case) and for each uncovered arc find its minimum distance to the point P (this can be done geometrically or by parameterizing arcs with cosine and sine and differentiation; anyway this can be done in O(1)).

What is bad about this solution is that the answer isn't a continuous function of circle radii and coordinates of their centers (some "inner" gap in picture can disappear after increasing all radii slightly), so avoiding stumbling in precision issues is really difficult). If all coordinates are integers doing everything precisely with numbers of form a + b sqrt(c) is probably the best way (you need to compare numbers of such form for sorting, this can be done by some squaring).

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Thanks for your comment! I think this solution will work. But finding union of covered arcs and then finding uncovered arcs which are not covered by any circle is not clear to me. How will you do that in n logn ? Maybe a good implementation. But I am not getting it.

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it +8 Vote: I do not like it

      Basically, we want to solve following problem: given n arcs on a circle that may intersect, find their union in form "union of non-intersecting arcs" (there will be no more than n arcs in such representation) in time.

      If any arc coincides with the whole circle, the union also is the whole circle.

      For convenience let's say that points on the circle have "coordinates" from range [0, 2π): a coordinate of point P is oriented angle between OP and horizontal axis, where O is the center of the circle. Every arc can be traversed in counterclockwise direction in exactly one way. Let's define the "start" of an arc as the first point of the arc when traversing it in counterclockwise direction and the end of an arc as the last point in counterclockwise traversal.

      First thing we do is reduce the problem to the problem on segment [0, 2π] instead of circle. Basically, we will cut the circle in one point and deal with arcs passing through this point accurately.

      Each arc can be written in form [l, r], where l is the coordinate of the arc's start and r is the coordinate of the arc's end. If l ≤ r, this arcs corresponds simply to a segment [l, r] after reduction. Segments [l, r], where r > l correspond to two segments [l, 2π] and [0, r] after reduction. It is easy to see that the union of arcs corresponds to the union of segments after reduction.

      Now we want to solve the same problem on line: we are given m = O(n) possibly intersecting segments and need to find their union in form "union of non-intersecting segments" in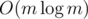 time.

      Let's say that we given segments are [l1, r1], [l2, r2], ..., [lm, rm]. By sorting we may assume that l1 ≤ l2 ≤ l3 ≤ ... ≤ ln. Now we will process segments [li, ri] in order of increasing i and keep current answer (union of all processed segments so far in "normal form", which is list of non-intersecting segments sorted in increasing order of their left ends (or their right ends, this is the same)).

      Current list may be empty, but in this case i = 1 and we just need to add [l1, r1] to the list. Otherwise, let [L, R] be the segment on the end of the current list (rightmost segment in current answer). Firstly, L ≤ li because L is left border of some previously processed segment. So, there can be only two cases:

      1. L ≤ li ≤ R. Then [li, ri] intersects segment [L, R] from current answer and only it (because all other segments in current answer end strictly before L and therefore before li). Then we just change the segment on the top of list from [L, R] to [L, max(R, ri)] (union of [L, R] and [li, ri]).

      2. R < li. Then we add [li, ri] to the end of list, because it does not intersect any segment that it is in the list currently.

      Actually this part is quite easy, just explaining it 100% formally made it sounding too complicated. It can be done with following code:

      struct seg 
{
    int l, r;
    bool operator < (const seg &o) const 
    {
         return l < o.l;
    }
};
vector<seg> v; // we want to find the union of segments in v, v may even be empty.

...

vector<seg> union;
sort(v.begin(), v.end());
for (int i = 0; i < (int)v.size(); i++)
{
    if (!union.empty() && v[i].l <= union.back().r)
        union.back().r = max(union.back().r, v[i].r);
    else
        union.pb(v[i]);
}
// I did not test this but it seems to be correct.

      TL;DR: cut the circle in some point and solve the same problem on the line; to solve the line version of the problem process segments in order of increasing coordinates of left ends and just update current answer.

      → Reply