Competitive Programming is all about the thrill of pitting yourselves against other coders and seeing who comes out on top. And in general, there’s nothing quite as fun for our community as putting on our coding hats and flexing our fingers over our keyboards and getting down to solve an interesting problem.
But competitive programming, like every sport, also has its World Cups. And for the CP community, the International Olympiad in Informatics is one such event that we all look forward to, not only as players but also as spectators. An annual competition that began in 1989 in Bulgaria, the IOI has risen from its humble beginnings to become one of the largest worldwide competitions for secondary school students that tests their skills in programming and problem solving.
Only the very best make it to the IOI Training Camps and eventually, the finals. Many of us have always wanted to see what the competition is like but the chance is given only to a select and deserving few. Fortunately for the entire community, CodeChef is bringing the Indian IOI Training Camp experience to you on our platform.
So what is an Indian IOI Training Camp? The Training Camp is probably one of the most enriching experiences any competitive programmer can have. The camp has two aims : it narrows down the pool of participants from a country from around 30 to 4 final participants, and it also trains and tests the participants so that they are ready for the big stage.
And it is this test that CodeChef is bringing to you. We are conducting a replay of the Indian IOI Training Camp, in the same format. There will be three challenging problems and a five-hour time limit for solving them. Three Team Selection Tests were conducted in May for the selection of Indian IOI team. This contest is the first among the three replays that we plan to conduct.
We’re sure you’re as hyped about this contest as we are. How do you take part? It’s simple, just register at CodeChef if you haven’t done so already, and check out the details below! We’re looking forward to seeing you all experience the thrill of the Training Camp selection tests.
The authors of the round are: - Arjun Arul (arjunarul), Praveen Dhinwa (PraveenDhinwa), and Sidhant Bansal (sidhant)
The testers panel consists of: - Rajat De (rajat1603), Sampriti Panda (sampriti), Kushagra Juneja, Swapnil Gupta (born2rule), Sreejata Kishor Bhattacharya (AnonymousBunny), Animesh Fatehpuria (animeshf), and Arjun P (Superty)
Duration: 5 hours
Start Date: Friday, 22nd June, 2018 at 19:00 HRS (IST)
End Date: Saturday, 23rd June, 2018 at 00:00 HRS (IST)
Contest Link: https://www.codechef.com/IOITC181
The time in other timezones can be seen here
Good luck!
Cheers, Team CodeChef











Gentle Reminder: The contest starts under half an hour.
a binary value output with just a single test case https://www.codechef.com/IOITC181/problems/KPERFMAT with all test case status revealed. very nice, i make 50 submissions and get 100 very coool
i wonder if this was the same in real selection test or not.
They were hacking solutions during or after contest in TSTs so this was not possible then. Even if that was not the case, I think it would be pretty difficult to get the AC this way.
nice to know it didn't passed in real TSTS.
But but "I think it would be pretty difficult", presenting top 4 AC solution:
https://www.codechef.com/viewsolution/18965679 https://www.codechef.com/viewsolution/18965825 https://www.codechef.com/viewsolution/18965740 https://www.codechef.com/viewsolution/18965633
VERY NICE RATED ROUND!!!!
Will there be any editorial?
Brief solutions:
Binary search on answer. To check whether a maximum distance D is possible or not, first let the point on the first segment be on R_1. Now assign the positions greedily: if point i is at ti, let point i + 1 be at ti + D. There are three cases: ti + D < Li + 1,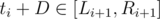 and ti + D > Ri + 1. In the first case just set ti = Li, in the second case do nothing, and in the third case you have to subtract ti + D - Ri + 1 from a suffix of the currently fixed points. If for some j tj becomes less than Lj the answer is no. Otherwise check that the distance between tn and t1 is atleast D.
and ti + D > Ri + 1. In the first case just set ti = Li, in the second case do nothing, and in the third case you have to subtract ti + D - Ri + 1 from a suffix of the currently fixed points. If for some j tj becomes less than Lj the answer is no. Otherwise check that the distance between tn and t1 is atleast D.
Take a spanning tree. If the remaining graph is bipartite you get a 4 coloring, otherwise you get a good cycle.
Consider the following problem first: given a bipartite graph and a perfect matching, print another perfect matching if it exists. This can be solved in linear time. Now start with an arbitrary matching M and produce another matching M'. Take an edge (u, v) which is in exactly one of M and M'. You can split the set of perfect matchings into two sets: those which contain (u, v) and those which don't. A recursive algorithm now works: let f(G, k) denote the answer for G and k, The recursion will call f(G', k1) and f(G", k2) where G' is the graph with the edge (u, v) removed (corresponding to perfect matchings not containing the edge) and G'' is the graph with vertices u, v removed (corresponding to perfect matchings containing the edge).
how do we check for the third case when t[i]+D>R[i+1] and whats the proof for the third case that we are subtracting t[i]+D-R[i+1] from the suffix of currently fixed points??
can you please explain KPERFMAT a little more?
In CIRCINT, how do you mean "from suffix of currently fixed points" ? You mean from all fixed points till now? Because we need to shift all of them back,right?
Will you move problems to practice?
problems are in practice now
please move problems to practice or at least upload the test data somewhere
So, was it rated, if so when will you update ratings?
ratings have been updated