Could anyone explain to me the proof for such a method of checking whether a number is primitive root or not http://zobayer.blogspot.com/2010/02/primitive-root.html
why should i check only certain numbers to be equal to one or not ?
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3856 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3462 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | -is-this-fft- | 162 |
| 3 | Dominater069 | 160 |
| 4 | Um_nik | 158 |
| 5 | atcoder_official | 157 |
| 6 | Qingyu | 156 |
| 7 | adamant | 151 |
| 7 | djm03178 | 151 |
| 7 | luogu_official | 151 |
| 10 | awoo | 146 |
Could anyone explain to me the proof for such a method of checking whether a number is primitive root or not http://zobayer.blogspot.com/2010/02/primitive-root.html
why should i check only certain numbers to be equal to one or not ?
| Name |
|---|



Since n is a prime, we know that gφ(n) = gn - 1 = 1. We want to know if there is another exponent e < n - 1 such that ge = 1.
Let e be the smallest, positive integer with ge = 1. This means that the exponents that give 1 are exactly 0, e, 2e, 3e, .... This means that e divides n - 1. If e is really smaller than n - 1, then there must exist a prime factor p of n - 1, such that e still divides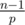 . Which means that
. Which means that 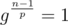 .
.
So it is sufficient to check if any of the terms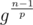 , with p prime and p | n - 1, is equal to 1.
, with p prime and p | n - 1, is equal to 1.