prudent's blog

[SOLVED] Property between XorSum and Sum of segment
By prudent, history, 6 years ago, In English

Question is solved, please ignore this post

Why if xor sum of segment is equal to sum of segment, this condition is also satisfied for all subsegments of original segment?
I know that it's true when all bits in numbers are unique, but is it the only case when it's true, and if it is, then why?

  • Vote: I like it
  • +5
  • Vote: I do not like it

»
6 years ago, # |
  Vote: I like it +1 Vote: I do not like it

Think about the binary representation of the bits. How is it possible that the xor sum is equal to the sum? If you figure that out, then it is obvious that this also holds for all subsegments.

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +1 Vote: I do not like it

    My friend told me that it's satisfied when all bits are unique. Yes that makes sense and it's true. But is it the only case when xorsum is equal to sum?

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
      ← Rev. 2   Vote: I like it +5 Vote: I do not like it

      Yes, of course. Assume that two numbers have the same bits set. Then in the xor sum these bits vaporize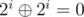 . And in the sum they add up 2i + 2i = 2i + 1. So if any bits are equal, then then the xor sum is guaranteed smaller than the sum.

      → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
          Vote: I like it +1 Vote: I do not like it

        Thank You very much, great explanation!

        → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
        ← Rev. 2   Vote: I like it +15 Vote: I do not like it

        I'd also like to add that the there's a relation between the functions sum & xor & and

        That is sum(a, b) = xor(a, b) + 2 * and(a, b)

        if looked closely at what Jakube said, if a = b then their xor would be 0 and all the bits that are both set (i.e. equals 1) in the binary representation of a, b that the xor function ignored because xor(1, 1) = 0 are accounted for by the and function because and(1, 1) = 1 and thus this value is shifted to the left by 1 bit (that is they get multiplied by 2)

        Hope this helps you visualize what's going on.

        → Reply
        • »
          »
          »
          »
          »
          6 years ago, # ^ |
            Vote: I like it +4 Vote: I do not like it

          OMG, I'm blown away, thank You!
          World of bits is so amazing!

          → Reply
        • »
          »
          »
          »
          »
          4 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          is there any such relation for more than 2 numbers?

          → Reply
          • »
            »
            »
            »
            »
            »
            4 years ago, # ^ |
            ← Rev. 3   Vote: I like it 0 Vote: I do not like it

            I guess it is easy to extend it, using bit manipulation. It's basically inclusion-exclusion.

            We can see that $$$ sum(a,b,c) = xor(a,b,c) + 2*and(a,b) + 2*and(b,c) + 2*and(a,c) - 3*and(a,b,c) $$$

            Because, if at a particular bit we have $$$0$$$ 1s or $$$1$$$ 1s, there is no problem, xor will cover that part of sum. When there are $$$2$$$ 1s in a particular bit, then xor will make it 0, so we need to add $$$2*and(a,b)$$$ for places that have bit in both $$$a$$$ and $$$b$$$, similarly other cases. Now, we see places where $$$a$$$, $$$b$$$ and $$$c$$$ all have bit set. Then, we have added that bit $$$6$$$ times, so we need to subtract $$$3$$$ of those.

            UPD: The correct formula is $$$ sum(a,b,c) = xor(a,b,c) + 2*and(a,b) + 2*and(b,c) + 2*and(a,c) - 4*and(a,b,c) $$$

            Look below for explanation and an example by Hossam

            → Reply
            • »
              »
              »
              »
              »
              »
              »
              4 years ago, # ^ |
              ← Rev. 2   Vote: I like it 0 Vote: I do not like it

              I think the last exclusion term should have a coefficient of 4.

              for example:

              $$$sum(1, 1, 1) = xor(1, 1, 1) + 2 * and(1, 1) + 2 * and(1, 1) + 2 * and(1, 1) - 4 * and(1, 1, 1) = 1 + 2 + 2 + 2 - 4 = 3$$$

              → Reply
              • »
                »
                »
                »
                »
                »
                »
                »
                4 years ago, # ^ |
                  Vote: I like it +3 Vote: I do not like it

                You are correct, what I missed was that, xor will also add that bit one time. So need to subtract 4 times.

                → Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Auto comment: topic has been updated by prudent (previous revision, new revision, compare).

→ Reply