How to calculate (a power b) mod p correctly if b is exceeding long long integer limit in c++.
→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3856 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3462 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | -is-this-fft- | 162 |
| 3 | Dominater069 | 160 |
| 4 | Um_nik | 158 |
| 5 | atcoder_official | 157 |
| 6 | Qingyu | 155 |
| 7 | djm03178 | 152 |
| 7 | adamant | 152 |
| 9 | luogu_official | 150 |
| 10 | awoo | 147 |
→ Find user
→ Recent actions
↑
↓
Codeforces (c) Copyright 2010-2025 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Feb/22/2025 20:19:35 (k2).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|











O(log2(b))?
yup!
Let b = b1b2.....bn(concatenated) By induction, Let x = a ^ (b1b2...bk) (mod p)
a ^ (b1b2....b(k+1)) = ( a^(b1b2....bk) ) ^ 10 * (a ^ b(k+1)) = x^10 * a^b(k+1)
now you can calculate modulo without overflow
got it! Thanks
first i need to store b. But b is exceeding the integer limit! How can i store b so that i correctly calculate (a power b) mod p. p is prime.
If b is in the form of a string, then we can calculate with the following code:
with the following code:
Now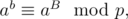 assuming that a is nonzero.
assuming that a is nonzero.
EDIT: This is exactly what DongwonShin wrote above. If b is being calculated via a DP table, then you can just take all values mod p - 1 and there won't be overflow.
got it. thanks!
but why p-1?
Fermat's theorem tells us that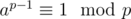 if (a, p) = 1. So we can take the power by the modulo.
if (a, p) = 1. So we can take the power by the modulo.
Thanks man!
In general if you have two co prime integers m and n, then m^p modulo n = m^(p%f(n)) modulo n, where f(n) is Euler totient function This.
For any prime n, f(n)=n-1.So, the Fermat's theorem follows from this.
I am using precomputed factorial and inverse factorial array to calculate b so should i use n-1 as the mod there also?
What if b is being calculated through nCr using precomputed factorial and inverse modulo arrays?Then also we've to use same mod p-1 ?
As long as your base(b) and p are co prime, I don't see why it can't be done. So, yes use same mod (p-1).
I tried but then for example 11*(inv[11)) didn't turn out to be 1 when i used p-1 as mod but while using p as mod it did show 1. here inv[11] = power(11,mod-2,mod) where power is fast exponential function.
What if b is calculated as a-c and c requires division operation?Then while using inverse modulo for division i should use which mod?I am confused.Please help.
Refer https://www.geeksforgeeks.org/find-abm-where-b-is-very-large/