The last online round of topcoder starts in less than 1h.
14 top coders qualify to the finals.
Let's discuss the problems after the contest!
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3857 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3463 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 165 |
| 2 | -is-this-fft- | 161 |
| 3 | Qingyu | 160 |
| 4 | Dominater069 | 158 |
| 5 | atcoder_official | 157 |
| 6 | adamant | 155 |
| 7 | Um_nik | 152 |
| 8 | djm03178 | 151 |
| 9 | luogu_official | 149 |
| 10 | awoo | 148 |
| Name |
|---|



I'm extremely disappointed with the quality of problems. This is TCO round 4, the most important round in a year. However both med and hard were pure implementations. TCO is not like this.
I won't pretend I'm ecstatic with this problem set, the truth is that I used the best what I had available. I would very much welcome people willing to write problems for future rounds of this calibre, and I will be posting calls for tasks in the future. Once I've had more time as the algo coordinator for TC, I hope to have a non-zero amount of unused hard problems available for rounds like this one, sadly, that isn't the case yet. If any of the participants of this round want to take a shot at writing or testing problems for the upcoming TCO rounds (or just an SRM), please get in touch with me.
That being said, I think you are being a bit unfair to the problems.
Obviously, difficulty is subjective, and I'm sure that to you both seem "pure implementations" because you saw the other steps immediately. I don't think you can blankly assume that about the rest of the field. (See the spread of solution times on the 250, for example.)
Personally, I like the 800. In particular, I think that coming up with a good way to "compress" the simulation is a cute ad-hoc step, and to me that's more valuable than just applying a named algorithm.
As for the 700, the reason why it was worth less is precisely because it's heavier on the implementation side, and also I like it less. But still there are many wildly different ways to implement it, including some approaches that are based on wrong ideas. Some of those lead to much shorter and simpler implementations than others, and coming up with such an approach is also a skill. (And recognizing that you should spend time looking for such an approach is another skill.) The problem also offered many challenge opportunities, in particular if you spent time thinking about incorrect approaches people may use.
Thanks a lot for running TopCoder rounds, and thanks for the very good points about these problems being interesting in their own ways! I agree that they test an important skill, too.
Still, my point (and maybe rng_58's) is that one of the best feelings one can get during programming contests is the one when, after solving a problem, you think "wow, before this round I would not expect this to be solvable at all, and now I could do it in 30 minutes!" (as a recent example that's still in my mind, consider this AtCoder problem). Of course, just this feeling is not enough (otherwise we might get something like IMO), but it's nice to experience this feeling together with the other good feelings like the one you mention — "wow, this neat trick makes the implementation faster and less bug-prone!".
So I'm hoping that we can experience the former feeling again at TopCoder!
Still, my point is that one of the best feelings one can get during programming contests is the one when, after solving a problem, you think "wow, before this round I would not expect this to be solvable at all, and now I could do it in 30 minutes!"
Oh absolutely. I know and love the feeling, I love such problems, and I hope to bring some to the finals :)
Hopefully we'll get some among the hardest SRM problems as well. That's the place where they belong.
(One thing that makes having such problems at the TCO finals a bit easier is that some problems cannot be used in online rounds because of the power of Google :) )
We definitely don't want to take TopCoder into another direction, the focus of algorithm competitions should still be on algorithmic problem solving, and in general you should expect the same type of problems as before.
I just feel that I personally have a bit broader definition of "algorithmic" than many other top contestants do. Sometimes we miss other nice things if we focus too narrowly on one of them.
Finding faces of planar graph is a classical problem. The only "original" part in this problem is processing the input, and the only difficult part in it is noticing that empty cycles may cause problems.
As misof points out, here we can use different implementations that are in some aspects easier than the general finding faces approach. For example, I've used the fact that the perimeter of the figure is small to use a scanline and a simple DSU on vertical 1xk blocks — this approach does not have any corner cases.
I think you overestimate the difficulty of finding faces in planar graph. First, you need to build the graph itself, which in this case is easy. Second, for each vertex all outgoing edges should be sorted by angle, which is much easier in this problem than in general, since we only have 4 directions. Next, you choose some unused edge, and while the current edge is unused, you go to the adjacent edge from u to the left from our edge. This process is like finding cycles in permutation. There can be degenerate faces as well as the infinite face, but they all have nonpositive area, so it's easy to check them.
is unused, you go to the adjacent edge from u to the left from our edge. This process is like finding cycles in permutation. There can be degenerate faces as well as the infinite face, but they all have nonpositive area, so it's easy to check them.
I agree that if you don't know this algorithm, then there can be a lot of interesting approaches to this problem. But if you know it, then this problem is just implementation and checking 1 case.
My opinion for 800 was biased because I solved it in a complicated way:
My solution was as follows. We start with the sequence A0, ..., An - 1. After one step, it will be Ab, ..., An - 1, A0 + ... + Ab - 1. After more steps, it will be more complicated, but we can always split the sequence into small number of pieces such that each piece follows a simple pattern. Thus, we can simulate the steps: we always keep the entire sequence (with some compression) and perform s steps, possibly simulating multiple steps at once when we can. This is a correct solution and getting the rough idea is easy (at least as a R4's hard), but there are lots of details in the implementation (my code ended up with 250 lines).
A much better way is to regard it as a variation of Josephus's Problem. Define a function f(n, k) that returns the range of elements we get in the k-th step when we start with n elements. Then it will be as simple as the original Josephus's problem. This solution looks more interesting.
Still, personally, finding an idea to a problem that is otherwise unsolvable is more interesting than finding a way to simplify implementation.
Last but not least, I grew up with old TopCoder problems and I'm a big fan of you. I'm looking forward to your problems!
Implementation on 800 really isn't that bad; I actually spent a fair amount of time going through the formulas. I think the only observation is that partial sums of a linearly recursive sequence are also linearly recursive (with one higher degree).
My only issue on 800 was checking s(b - 1) ≥ n - 1. I did this wrong... I tried b - 1 ≥ (n - 1) / s to avoid overflow but this caused division by 0 when s = 0. Fixing that gets AC. :(
I don't think implementation in 800 was all that important — matrix algebra is a standard thing and the rest is more about figuring out how to efficiently represent the numbers so that they could be summed up quickly.
700 was just nope.
Hmm...
How many people fail 700pt problem just because output full array of A like me?
P.S. I check all codes and found I am the only one...
Sorry :( Initially I did not spot the bug, but then I opened another solution which handled first 100 and last 100, and remembered that I did not see this logic in yours.
I think if you didn't hack me, I will fail system test still. >__<
I can laugh at myself that I cannot attend final round just because of format error for a year. XDDDD
So sorry about that :(
We are working within the limitations of the backend, and "hacks" like this one are sometimes needed to make a problem work. (Inputs and outputs need to be kept small enough.)
I hate seeing people failing because of these technicalities.
I'll add an item to my checklist to make sure that hacks like this one are covered by an example in the future. I know it won't help you now, but hopefully it will at least save someone else later.
Am I the only one who thinks that processing the input correctly for the 700 pt problem was the hardest part? D:
Nah. Writing the input data validator ("checkData" in TC lingo) was the hardest part. I had to do the parsing and handle all possible cases where it may fail :D
You actually had the easy version :)
Without the validity checks a recursive parser can be written quite quickly and easily:
About 10 lines of code in my C++ brute force solution I wrote locally.
I'm wondering does such parser works in O(result_string * input_string)? E. g. on string like
FFF...FFF240000F?It should do ~500 millions of operations if 5th step implemented naively.
Or 500 millions is ok?
The reference solution has a StringBuilder and appends to it as it goes (and stops if it gets too large), so that one should be fine complexity-wise. In C++ I think those 500M operations may be fast enough, but I haven't tried. You still have a valid point that what I described above isn't the most efficient implementation possible.
My solution for 800 is quite simple. I like this problem in itself.
Let's consider an infinite sequence S = {1, ..(n times).., 1 / b, ..(n times).., 1 / b2, ...}.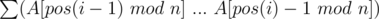 while pos(x) is the position such that
while pos(x) is the position such that  .
.
Then the 1 step of operation can be regarded as "remove elements from the front of S until the sum becomes b".
In other words, the value of i-th removed element is
It needs some idea to implement without fractions but it can be very short code.
The main part of the code:
sum(l, r)is a function calculates