xennygrimmato's blog

Calculating time complexity for CEOI 2018 — Toys (Day 2)
By xennygrimmato, history, 6 years ago, In English

I am trying to estimate the upper bound of the time-complexity of this solution by ksun48. Currently, I am assuming the upper bound on the number of divisors of N to be 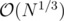based on this codeforces blog, but that fact doesn't simplify the calculation of time complexity here.

  • Is there a simple way to estimate a good upper bound for this solution?
  • Is there some literature around formally calculating time complexity in such scenarios?
  • Vote: I like it
  • +28
  • Vote: I do not like it

»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Auto comment: topic has been updated by xennygrimmato (previous revision, new revision, compare).

→ Reply
»
6 years ago, # |
← Rev. 2   Vote: I like it +8 Vote: I do not like it

In problems like this often you just want to run your solution on a big test to see how fast it works. I don't think a tight bound can be found in this problem.

And a big test is something that has many divisors, so likely 2·2·2·3·3·5·7·11·13·... or similar is the worst case.

→ Reply
»
6 years ago, # |
← Rev. 2   Vote: I like it +1 Vote: I do not like it

Edit: I analyzed the code incorrectly, since the solution also keeps the last divisor it divided by. Still, I think the approach below can help, so I'll just keep that here.

If we mark the time complexity as T(n), then following the solution you linked, we get the recurrence:

A nice way to analyze this would probably be to look at the exponents in the prime factorization, since then our recursion splits to all subsets of the exponents in the prime factorization (for instance, 2251 splits to 2151, 51, 22, 21, 1). At the moment I'm not sure how to track this, but we can look at a specific easier case, for instance n = 2m. In this specific case, the recurrence is:

and we can see that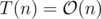 for the case when n is a power of 2. 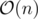is already not very optimistic for a problem that has n up to 109... fortunately the constant should be pretty low.

→ Reply