Harolinch's blog

(help) relation between hashes and graphs
By Harolinch, history, 6 years ago, In English

i'm try to solve this graph problem (double profiles) and it requires to use hashes in order to solve the problem.

first of all, i didn't solve the problem and and if anyone could give me help, i appreciate that.

secondly, when should i know that i need to use hashes to solve a graph problem (what is the properties of the graph problems that need hashes)

  • Vote: I like it
  • +5
  • Vote: I do not like it

»
6 years ago, # |
← Rev. 27   Vote: I like it +7 Vote: I do not like it

The hash approach seems to be related to the more abstract problem of equality checking of a pair of subsets Si and Sj of V = {1, 2, ..., n}.

Hashing should find the answer to the equality checking Si = Sj indirectly by computing the hash key h(Si) for each subset, and then checking if h(Si) = h(Sj), provided that the no collision takes place, i.e. no pair (i, j) exists, where i ≠ j, such that Si ≠ Sj and h(Si) = h(Sj). In other words, the hash key function should be a one-to-one mapping that enumerates the existing distinct subsets of V by assigning them distinct identification numbers which can be checked for equality more efficiently.

The solution of the original problem should then be equal to the cardinality of the set of pairs P = {(i, j)|1 ≤ i ≤ n - 1, i + 1 ≤ j ≤ n, h(Si) = h(Sj)}.

In test case 1, for example,

  1. When checking the pair (1,2): S1 = S2 = {3}. Therefore, 1 and 2 are doubles.

  2. When checking the pair (1,3): S1 = S3 = {2}. Therefore, 1 and 3 are doubles.

  3. When checking the pair (2,3): S2 = S3 = {1}. Therefore, 2 and 3 are doubles.

In all cases, if i and j are friends, their friendship is not included in the neighborhood when checking if i and j are doubles.

→ Reply
  • »
    »
    6 years ago, # ^ |
    ← Rev. 3   Vote: I like it 0 Vote: I do not like it

    thanks so much, if you understand how problem reduced to the fact that you want count the pairs of equal subsets, please help me understand it ...

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
      ← Rev. 3   Vote: I like it +1 Vote: I do not like it

      With pleasure.

      The counting part should be as simple as follows. Suppose that the hashing procedure for all subsets in S ends up with generating k distinct hash keys h1, h2, ..., hk, where the corresponding distinct subsets exist n1, n2, ..., nk times in S, respectively, and .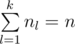

      Then, the total number of unordered pairs in the original multi-set where Si = Sj should be equal to .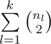

      → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        I understand how is the counting part done, what i'm not understand is "why"

        why in the problem should i count the number of pairs of equal subsets ... what is the proof of correctness

        → Reply
        • »
          »
          »
          »
          »
          6 years ago, # ^ |
          ← Rev. 12   Vote: I like it +1 Vote: I do not like it

          Alright.

          In the problem statement, "Let's say that profiles i and j (i  ≠  j) are doubles, if for any profile k (k  ≠  i, k ≠  j) one of the two statements is true: either k is friends with i and j, or k isn't friends with either of them.", implies that profiles i and j are doubles when both have the same neighbors, i.e. the same set of friends.

          If profile k exists such that it is a friend of i but not a friend of j, or vice versa, then i and j are not doubles__ by definition.

          → Reply