Spoiler
I tried to solve problem A from the Google CodeJam finals 2018, after reading the analysis.
In the analysis it says: We can binary search for L and U independently using their original definitions, which yields an algorithm that takes time O(S5 × log(R × C))
I don't understand how they arrive at this bound. The compressed graph has O(S2) vertices and O(S3) edges. Running Edmonds-Karp in each binary search iteration would therefore give a complexity of O(V × E2) = O(S8). Running Dinic would give O(E × V2) = O(S7). How do they get S5?
I implemented a solution both with Dinic and using Edmonds-Karp. Dinic was accepted, Edmonds-Karp got TLE for the large problem.











In theory, you could use an algorithm by V.King, S.Rao and R.Tarjan running in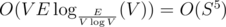 .
.
In practice, you're probably better of using push-relabel running in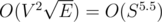 . (My solution with it was fast enough even with two log factors and using
. (My solution with it was fast enough even with two log factors and using
__int128in the flow algorithm due to worse flow graph modeling.)