theDarkShadow's blog

help me to increase my level
By theDarkShadow, history, 6 years ago, In English

Which Algorithms and Data Structures should I have to learn to solve C and D level problem......... help me :D

  • Vote: I like it
  • -18
  • Vote: I do not like it

Comments Comments (15)
| Write comment?
»
6 years ago, # |
  Vote: I like it +6 Vote: I do not like it

The only data structure you need to use is your brain. The only algo you need is to think.

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +57 Vote: I do not like it

    You are being downvoted but (aside of your tone) you are at least partially right.

    Solving problems is a lot less related to implementing standard algorithms and structures than some people realize. Don't get me wrong, I've regularly had to solve problems that depended on algorithms that I couldn't possibly invent on my own. But let's have a look at the last 5 C and D level problems (skipping the Div 3 and the Educational that I didn't participate in).

    1037C - Equalize: An ad-hoc string problem. I don't think there is any standard algorithm at play here. The problem reduces to making a few observations about which operations are ever profitable.

    1037D - Valid BFS?: Well, this one clearly already mentions an algorithm: the BFS. It teaches you how it works, but it probably helps a lot if you already have built intuition about that. No other standard algorithm is needed to solve the problem.

    1028C - Rectangles has a lot of variations in how to solve it, but the one I implemented did not use any particular standard algorithm. If you count "calculating prefix minimums" as an algorithm then maybe, but that is a stretch.

    1028D - Order book: I used a segment tree but that is not at all necessary or even that useful. Most solutions "simulate" the process one way or another, mostly using something like std::set. While it is a data structure, it is not one you actually have to implement.

    1025C - Plasticine zebra: Another ad-hoc string problem. Once again, you have to make an observation of what the operation does (or rather: what the operation is in other words). No standard algorithm is necessary.

    1025D - Recovering BST: Here you'll probably need to know how dynamic programming works. Intuition about binary search trees helps. Nothing else is necessary.

    1023C - Bracket Subsequence: This is a problem with a greedy solution. No standard algorithm is necessary.

    1023D - Array Restoration: Once again, I used a std::set<int> for something. In other parts of the problem, no standard things were necessary.

    1020C - Elections: Another greedy problem. Or, almost brute force even. Nothing standard to be seen.

    1020D - The hat: Well, this one is binary search.

    In short, almost none of the so-called standard algorithms or data structures are actually necessary for these 10 problems. In particular, none of the C level problems used anything. Only one D asked you to implement a standard thing, two of them require some knowledge of C++-s library and two of them only require intuition about something.

    While it is important to learn algorithms, it is more important to learn problem solving skills. Training your intuition, gaining experience (a lot of the solutions contained "little bits" from earlier problems) and "thinking skills". So, to get to a higher level, just solve problems and don't worry so much about what algorithms you don't know. Instead, learn those on the fly.

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it +22 Vote: I do not like it

      Exactly! I can see why are you a yellow coder — you have got the gist of what is important (a creative mind) unlike the regular div 2 coder that thinks that there is some magic data structure/algo that is needed for every problem. Lol. No wonder these people never improve and they even wonder why! Rofl.

      → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
          Vote: I like it +33 Vote: I do not like it

        you are absolutely right. you shouldn't have a lot of downvotes, but people don't want to see the truth!

        → Reply
        • »
          »
          »
          »
          »
          6 years ago, # ^ |
            Vote: I like it +39 Vote: I do not like it

          My opinion is that people would be more receptive to the truth if it was presented more tactfully. While I think that Lance's "brutal honesty" is a conscious decision, I'm not sure that is the best way to tell those things to people.

          → Reply
          • »
            »
            »
            »
            »
            »
            6 years ago, # ^ |
              Vote: I like it 0 Vote: I do not like it

            I agree to you, if you know algorithms that do not mean that you can solve hard tasks, C and D tasks, but if you do not know any algorithms you can not solve big number of D tasks, so you need to study algorithms too, see Twice.Dahyun's comment.

            → Reply
»
6 years ago, # |
  Vote: I like it -8 Vote: I do not like it

DP, greedy, binary search, DSU, DFS, BFS, dijkstra, LCA, hash, math, probability, RMQ, IT, BIT, queue, deque, stack, map, set

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it -12 Vote: I do not like it

    you can also look at the tag of the previous C D problems to know what to learn too

    → Reply
»
6 years ago, # |
  Vote: I like it +27 Vote: I do not like it

These graphs might help.

Topic Distribution for C

Topic Distribution for D

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +14 Vote: I do not like it

    Something is fishy here. I did not find a single Div2C with FFT as a tag.

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it +11 Vote: I do not like it

      I think it says C as in all divisions C.

      There is a sole C problem that has an fft tag and that is 662C - Binary Table

      Source: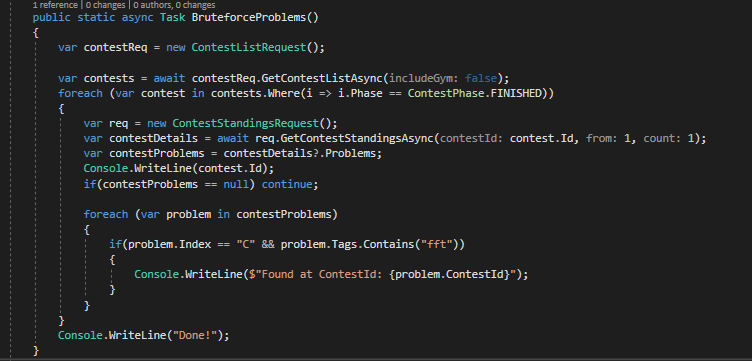

      → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        To generate the graphs I used the codeforces API collect all problems and separate their tags into based on their index. I couldn't figure out a simple way at the time to separate div 2C and div 1C and div 2D and div 1D. So they are lumped together. I was hoping Div 2 only contests are common enough that the general topic distribution will be correct even with noise from other contests. Now I realise there is a relatively simple way to separate into div 2 only.

        → Reply
»
6 years ago, # |
  Vote: I like it -7 Vote: I do not like it

Smart people can use simple data structures to solve those C and D level problems. Being a stupid person, I need to use FFT, Persistent Treaps, Centroid Decomposition on Edges, Heavy-Light-Medium Decomposition, and Voronoi Diagrams to solve those problems. If you are unable to solve those C and D level problems now, I suggest you to learn those advanced algorithms and data structures.

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +16 Vote: I do not like it

    An example:

    If you have an array A and you want to find the prefix sums, it can easily be done with advanced algorithms like FFT. Create one polynomial A(x) = A1x^0+A2x^1+...+Anx^(n-1) and another polynomial B(x) = x^0+x^1+...+x^(n-1). The coefficients of A(x)*B(x) are your prefix sums. In particular, A(x)*B(x) = A1x^0+(A1+A2)x^1+(A1+A2+A3)x^2+...

    → Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it -13 Vote: I do not like it

    Being a grandmaster doesn't mean you have to boast your skills every time. And he most likely meant div2C and D, not their div1 counterparts.

    → Reply