having a point p1(x0, y0) and want to find the projection of p1 on the line L given in form ax + by + c = 0
let the projection point is p2(x1, y1), so how to find x1 and y1 ?
i have a code segment which do so but i don't understand it, so can someone help me to understand it ?
the code is
point closest_point (line l, point p)
{
double k = (l.a * p.x + l.b * p.y + l.c) / (l.a * l.a + l.b * l.b);
return point (p.x - l.a * k, p.y - l.b * k);
}










The projection is simply the intersection point of two perpendicular straight lines:
ax + by + c = 0
and
b(x - x0) - a(y - y0) = 0
where the latter line passes through (x0, y0). Instead of solving the two linear equations for x and y directly to compute the intersection point, your code segment uses a parametric approach. As the direction of the normal line is [a b], the second equation is replaced with two parametric equations in terms of the parameter k:
x = x0 - ka
y = y0 - kb
Substituting for x and y from these two parametric equations in the first equation gives one equation in the parameter k
a(x0 - ka) + b(y0 - kb) + c = 0
whose solution is the desired value of k at the intersection point
k = (ax0 + by0 + c) / (a2 + b2)
i saw this equation b(x - x0) - a(y - y0) = 0 before on the internet but i didn't understand it, where it comes from, can you explain it to me.
what i Know about my code segment is ...
the the distance between a point and line is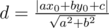 .
.
the norm of line is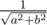 .
.
can you continue on this ?
The second equation is derived from the fact that the two straight lines:
are perpendicular for any |a| + |b| > 0, and any c and d, where a, b, c and d are real numbers.
The proof is simple as the normal vectors of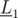 and
and 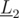 are
are
The dot product of the two normal vectors is
Therefore, the two lines are perpendicular. Note that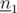 and
and 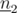 have the same norm, and can be normalized, i.e. transformed to orthonormal vectors, by dividing each component by
have the same norm, and can be normalized, i.e. transformed to orthonormal vectors, by dividing each component by  .
.
k is just the parameter used in the two parametric equations to find the intersection point as mentioned before.
It can be shown from the two parametric equations that
b(x - x0) = a(y - y0) = - kab
Therefore,
b(x - x0) - a(y - y0) = 0
Finally, if orthonormal vectors are used in the parametric equations, then k = d at the intersection point of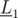 and
and 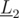 , where d is the minimum distance between the point (x0, y0) and
, where d is the minimum distance between the point (x0, y0) and 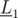 .
.
The following is an update for
closest_point()when orthonormal vectors are used.Sample Test
Input:
3 4 -5 0 0
Output:
0.6 0.8
=====
Used: 15 ms, 140 KB
thanks so much for your help, i'm somehow trying to put all together,
you seemed to understand it well, and that's why can you help me understand what is the relation between A and B and C in line equation Ax + By + C = 0.
seems there are a lot of relations, one of them is the slop and the slop of perp. what else could you show me ?
With pleasure. Algebraic approaches to geometry are among my favorite topics in Math.
RE: What else?
You can read more about analytic geometry in the following reference.
An Algebraic Approach to Geometry