So I came up with this problem yesterday, which I couldn't solve. With a quick google search I found nothing relevant so I thought I could ask here for help.
The Problem
You are given a tree T with n nodes and an integer k. You are asked to find the length of longest path in T which has exactly k inversions. Here we define path inversions for a specific path P as the number of inversions in the array of the nodes visited in P, in that order. If there is no such path output - 1.
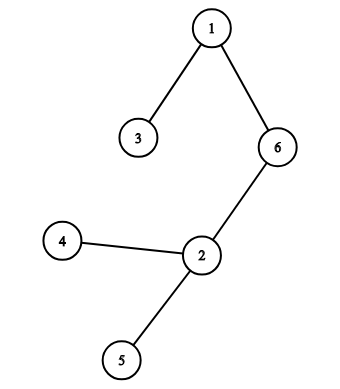
Let's consider the above tree for example, with k = 2. The answer is 4 since the path 1 - 6 - 2 - 5 has exactly 2 inversions. Note that the path 5 - 2 - 4 also has 2 inversion however it isn't the path with the maximum length.
I am looking for solutions with complexity better than O(n2·logn)
Thank you for your time.











You can achieve O(n2 × logn) launching DFS from each node and counting inversions using Fenwick tree.
Yeah I already figured that out. n3 is a typo in post. Fixed. Thanks anyway.
"Two elements a[i] and a[j] form an inversion if a[i] > a[j] and i < j" Isn't that the definition of inversion? Do you mean 5->2->4 instead of 4->2->5?
Yes. Fixed. Thank you