I was trying to calculate this for some integer n < = 109 :
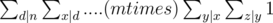
In other words, summation of summation of ... (m times summations) of divisors of n.
If anyone can help me out with this!
| # | User | Rating |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3831 |
| 3 | Radewoosh | 3646 |
| 4 | jqdai0815 | 3620 |
| 4 | Benq | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | gamegame | 3386 |
| 10 | ksun48 | 3373 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 164 |
| 1 | maomao90 | 164 |
| 3 | Um_nik | 163 |
| 4 | atcoder_official | 160 |
| 5 | -is-this-fft- | 158 |
| 6 | awoo | 157 |
| 7 | adamant | 156 |
| 8 | TheScrasse | 154 |
| 8 | nor | 154 |
| 10 | Dominater069 | 153 |
I was trying to calculate this for some integer n < = 109 :
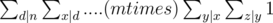
In other words, summation of summation of ... (m times summations) of divisors of n.
If anyone can help me out with this!
| Name |
|---|



Let's denote your summation by f(m,n).
First, prove that f(m,*) is multiplicative. This can be easily proved by induction, assuming f(m-1,*) are multiplicative, and obviously f(0,*) is 1, which is multiplicative.
Hence, factorise n into prime powers, and multiply the answers for individual prime powers.
So, now you only need to solve f(m,n) where n is of the form (p^a) where p is some prime.
Another observation tells you that p is irrelevant, only the value of 'a' matters, so let's call g(m,a) = f(m,p^a)
Writing the obvious recursion from g, by the given definition of f, we get
g(m,a) = g(m-1,0) + g(m-1,1) + ... + g(m-1,a)
with base case g(0,x) = 1
We can see that this is equivalent to distributing 'a' objects in 'm+1' places, where the recursion for g indicates looping on number of objects in the 1st place.
So, g(m,a) = C(a+m,m)
I believe this solves your problem. I might have missed something here or there or maybe did some off by 1 error, but the basic idea is this only, you'll get a bunch of C(n,r) terms and the function is multiplicative.
Perfect!
Auto comment: topic has been updated by S.Jindal (previous revision, new revision, compare).
xd