RedNextCentury's blog

Tishreen-CPC 2017 Editorial [GYM]
By RedNextCentury, 6 years ago, In English

First I would like to apologize for the error in the test cases of problem G. All solutions were rejudged and 3 teams/participants were affected, I am very sorry.

Also, thanks to Ashishgup for discovering the error.

I hope you enjoyed the problems in general, below is a brief description of the solutions (if you need a detailed explanation of some problem write in the comments)

Any feedback is appreciated :)

A. Printing Books

While the number of digits left is enough, increase X to the closest power of 10, and subtract the number of digits needed from N. Let's denote the number of digits in X as d(X) and the smallest power of 10 greater than X as p(X).


while (p(X)-X)*d(X) <= N
    N-=(p(X)-X)*d(X)
    X=p(X)
    ans+=p(X)-X

At the end, there might be some leftovers from N, if it is not divisible by d(X), then the answer is -1. Otherwise, add 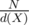to ans.

B. Ali and Wi-Fi

Let's say you want to join a subset of the given networks, to do this, you must stand in the area of intersection of all the circles of these networks. This area is enclosed by some arcs of the circles and points of intersection of these arcs, the area always contains points of intersection between 2 or more of these circles, or a center of one or more of the circles. So it is possible to obtain the optimal answer at one of the intersection points or at the center of some circle.

This way, we need to check O(n2) points (n centers, and at most 2 points from each pair of circles). To check each point, we go through all circles and store the speeds of the circles that cover this point, then sort these speeds and take the maximum m speeds.

Complexity: O(n3log(n))

C. Shahhoud Training Hussain

Each day, Hussein receives K problems, and solves min(P, K) of them. So he will miss K - min(P, K) problems everyday.

Since we have N days, the answer is N * (K - min(K, P))

Complexity: O(1)

D. Largest Group

For each girl, calculate the mask of the boys that this girl is friends with. Now for each one of the 2P possible subsets of girls, calculate the bitwise AND of the masks of these girls, the number of 1's in the binary representation of the resulting number is equal to the number of boys that are friends with each of the chosen girls, we add it to the number of chosen girls and we get the answer for this subset. Find the maximum answer between all subsets.

Complexity: O(2PP)

E. Minesweeper

This problem can be solved using backtrack or DP Bitmask, I will explain the DP solution:

Let's add rows one by one. We represent a row using a mask (0 if its a mine, 1 if its a free cell).

In order to know which mask can be added as the current row, we need to know the masks of the 2 previous rows, and check that the last row can be placed between the current mask and the one before the last.

So we have dp[i][mask1][mask2] is the number of ways to set the first i rows, with the last 2 rows being mask1 and mask2. To calculate it, we loop through all valid masks for the new row and add dp[i + 1][mask2][newMask].

The only thing left is to write a function that takes 3 masks, and checks if the middle row does not violate any of the rules when placed between the other 2 masks.

Complexity: O(rc23c)

F. A Missing Problem in TCPC2017

There are many ways to solve this problem, either mark the available problems and then find the unmarked problem, or calculate the sum of the available problems and print n * (n + 1) / 2 - sum, or find the first i that is not equal to a[i] and print it.

Complexity: O(n)

G. Robots

Solution 1:

Sort the robots by xi, and go through them in decreasing order. Simulate the first query step by step and store in a set the value of edges that this robot goes through. Now for each query, starting from the node that the previous query ends in, keep going up in the tree and deleting those edges from the set until every element in the set is less than xi. After that, continue simulating the query going down step by step, adding the edges to the set.

Each edge will be added at most once to the set, and it gets deleted when it is larger than all x values left, so it won't be added to the set again.

Complexity: O(nlog(n))

Solution 2:

Sort the robots by xi.

If a robot xi and robot xj (xi < xj) pass through a node during their movement, then every other robot xk such that xi ≤ xk ≤ xj will also pass through this node.

We can start a dfs traversal at node 1 and keep the range of robots that will pass through this node. Then, in each node, we go through the children, and for each one find the range of robots that will go to that child. And also find the range that will end up in this node and add them to the answer.

Complexity: O(n + qlog(q))

H. Buying Products

For each shop, take the two cheapest products, and add them to a set.

The answer is the sum of the cheapest k products in the set.

Complexity: O(nlog(n) + k)

I. A Movie in Byteland

First give each name (ltr and rtl) a number according to it's order lexicographically among all names. and also store for each name whether is has an 'm' or not.

Now we have n pairs of numbers and we need to find the longest increasing subsequence, where a pair (a, b) is bigger than another pair (c, d) if a > c and b > d. We also need to satisfy the rule that any two consecutive names exactly one of them has an 'm' in it.

To solve this problem, we sort the pairs by the first value, then we only need the subsequence to be increasing by the second value.

Use two segment trees, one for the pairs that have an 'm' in it, and one for the pairs that don't. The rest is just like the ordinary nlogn solution for LIS. The answer for the pair that has an 'm' is calculated using the segment tree that doesn't have an 'm' and so on.

Complexity: O(nlog(n))

J. The Volcano Eruption

Create a graph where each circle is a node, and any pair of intersecting circles have an edge between them.

Let's find the number of components that have at least once circle that intersects with each side of the street, this component will cut the street, so we must use a suit to pass it. Therefore the answer is the number of such components.

Complexity: O(n2)

K. Poor Ramzi

Let dp[l][r] be the number of sumindromes that can be achieved from the range [l, r].

To calculate this dp, iterate through all possible prefixes [l, i] and suffixes [j, r] such that i < j and sum(l..i) = sum(j...r) and add dp[i][j] to the answer.

Also add 1 to dp[l][r] to consider summing all the range into one integer.

Complexity: O(n4)

L. Eyb0ss

First, we can calculate the sum of maximums alone, and the sum of minimums alone, then subtract them.

How to find the sum of maximums?

Let's consider the linear version of the problem, given n integers, find the sum of maximum numbers in each range [l, r].

To solve this problem, we go through each number and find the number of ranges where this number is the maximum.

We can find the closest number x greater than it before it and the closest number y greater than it after it using a stack.

The current number is the maximum in all ranges that start after x and end before y. We add to the answer the current number multiplied by the number of these ranges.

Now, let's go back to the 2D version.

For each pair of rows r1 and r2 (r1 < r2), we want to calculate the sum of maximums in all rectangles that start at r1 and end at r2. For each column, only the maximum number in this column between r1 and r2 can be a possible maximum in the rectangle. So we find the maximum number in each column and store them in an array, then apply the linear version of the problem on this array.

Note: to simplify the implementation, you can first calculate the sum of maximums, then multiply all the numbers in the array by -1, then find the sum of maximums again and sum the two answers.

Complexity: O(n3)

  • Vote: I like it
  • +20
  • Vote: I do not like it

Comments Comments (24)
| Write comment?
»
6 years ago, # |
  Vote: I like it +11 Vote: I do not like it

For problem D, I think there is a confusion between N and P. I guess you meant it can be solved in O(2^P P) instead of O(2^N N).

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +6 Vote: I do not like it

    Thanks, fixed now. I'm so used to N being the main variable in every problem :P

    → Reply
»
6 years ago, # |
  Vote: I like it +17 Vote: I do not like it

Problem D is about to find the maximum clique in the graph, so another nice solution could be to find the maximum independent set in the complement graph since these are oposite definitions. And the complement graph is bipartite so the cardinality of the independent set can be calculated using a maximum matching algorithm.

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Please, someone explain me the editorial of Problem B Ali and Wi-Fi.

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    This is what the common area between many circles might look like, it is always defined by points that are intersection points between 2 or more of these circles.

    Note that anywhere you move inside the red area, the answer will be the same, since you are still covered by the same subset of circles.

    Therefore, it is enough to check the answer at each intersection point. Except in the case where there are one or more circles inside each other, like this:

    Here, there are no intersection points, and the common area is the smallest circle, so we also need to check the answer at the center of each circle.

    How do we check the answer?

    For each point, go through all circles, if the distance between the center of the circle and the point is less than or equal to the radius of the circle, then this circle covers the point, add its speed to a set.

    At the end, take the maximum m speeds from the set, that is the answer for this point.

    Calculate the answer for each of the points and take the maximum.

    → Reply
    • »
      »
      »
      4 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Can you please share your code for this problem B. Thanks in advance _/_

      → Reply
»
6 years ago, # |
  Vote: I like it +3 Vote: I do not like it

In the problem G-Robots, I had used the Solution-2 technique, i.e, I am passing a range in the dfs. From each node I am passing on the correct ranges to its respective children using binary search. The range that is remaining is allotted to the node itself. Getting WA in Testcase 2. Can anyone please find out the mistake. Grateful !

#include<bits/stdc++.h>
#define ll long long int
using namespace std;
ll n,q;
vector<ll> ar,ans;
vector<vector<pair<ll,ll> > >g;
inline pair<ll,ll> bs(ll val,ll l,ll r)
{
    ll low=l,high=r,mid,ans=1e18;
    while(low<=high)
    {
        mid=(low+high)/2;
        if(ar[mid]>val)
        {
            ans=min(ans,mid);
            high=mid-1;
        }
        else
            low=mid+1;
    }
    if(ans==1e18)
        return {-1,-1};
    return {ans,r};
}
inline void dfs(ll nd,ll l,ll r)
{
    ll val,newnd;
    pair<ll,ll> p;
    for(auto &it:g[nd])
    {
        newnd=it.second;
        val=it.first;
        p=bs(val,l,r);
        if(p.first==-1)
            continue;
        dfs(newnd,p.first,p.second);
        r=p.first-1;
    }
    for(ll i=l;i<=r;i++)
        ans[i]=nd+1;
}
int main()
{
    ios_base::sync_with_stdio(0);
    cin.tie(0);
    ll t;
    cin>>t;
    while(t--)
    {
        ll u,v,w;
        cin>>n>>q;
        g.clear();
        g.resize(n);
        for(ll i=0;i<n-1;i++)
        {
            cin>>u>>v>>w;
            u--;
            v--;
            g[u].push_back({w,v});
        }
        for(auto &it:g)
            sort(it.rbegin(),it.rend());
        ar.clear();
        ar.resize(q);
        ans.clear();
        ans.resize(q);
        for(ll i=0;i<q;i++)
            cin>>ar[i];
        sort(ar.begin(),ar.end());
        dfs(0,0,q-1);
        ll cnt=0;
        for(auto &it:ans)
            cnt+=it;
        cout<<cnt<<"\n";
    }
    return 0;
}
→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it

    You are assuming that the edges are always given from the parent to the child, that is not true.

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it +8 Vote: I do not like it

      Thanks for spotting that out :) I corrected my solution. Now it is accepted

      → Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Could somebody help me solve problem H, please?

→ Reply
  • »
    »
    6 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    From each shop, you can only but 2 items at most, so the best option is to buy from the 2 cheapest items. So keep an array that has the two cheapest items from every shop, sort it, and the answer will be the sum of the first k elements.

    C++ Code

    → Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

why is the testcase 2 of problem D giving TLE?

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Is there a way to solve problem D with bigger constrains? ( Not 2^Something )

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

help me explain problem A, I really don't understand it?

→ Reply
  • »
    »
    6 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    The first case: 11 5 This pagination that starts at 5:

    5,6,7,8,9,10,11,12

    The total number of written digits is 1, to achieve thsi we are using 8 numbers.

    → Reply
»
6 years ago, # |
  Vote: I like it +7 Vote: I do not like it

How to solve Problem E using backtrack?

Since, for $$$r = c = 6$$$ and $$$m = 8$$$ there could be more than $$$10^{9}$$$ valid grids, how would we prune the search space?

→ Reply
»
5 years ago, # |
  Vote: I like it -8 Vote: I do not like it

Please, link this editorial to the contest

→ Reply
»
5 years ago, # |
  Vote: I like it 0 Vote: I do not like it

in problem A i tried solving it using binary search .. why it's giving me a WA? 61876758 did i miss anything ? RedNextCentury

→ Reply
  • »
    »
    5 years ago, # ^ |
      Vote: I like it +1 Vote: I do not like it

    Your binary search range is too small, when $$$X$$$ and $$$N$$$ are both around $$$10^{15}$$$ the final page number will definitely be larger than $$$10^{15}+100$$$

    → Reply