AtCoder Grand Contest 028 will be held on Saturday (time). The writer is maroonrk. This contest counts for GP30 scores.
Contest duration: 150 minutes
The point values will be announced later.
Let's discuss problems after the contest.
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3856 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3462 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | -is-this-fft- | 162 |
| 3 | Dominater069 | 160 |
| 4 | Um_nik | 158 |
| 5 | atcoder_official | 157 |
| 6 | Qingyu | 156 |
| 7 | djm03178 | 151 |
| 7 | adamant | 151 |
| 9 | luogu_official | 150 |
| 10 | awoo | 147 |
AtCoder Grand Contest 028 will be held on Saturday (time). The writer is maroonrk. This contest counts for GP30 scores.
Contest duration: 150 minutes
The point values will be announced later.
Let's discuss problems after the contest.
| Name |
|---|



3min
F is solvable in O(N2logN), so please try it.
My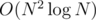 solution is slower than most of the O(N3) solutions:(
solution is slower than most of the O(N3) solutions:(
my implemention
Is there any way to distinguish them?
I have solved task A and I have read 'editorial', but could anyone explain the solution in his own words?
How to solve task B?
Basic idea is this: fix two specific elements i and j. The cost for removing block j will include the weight of i if and only if j is removed first out of the blocks in the section i through j. If not, i will be disconnected from j (or won't be present at all) by the time j is removed.
The number of permutations in which j is removed first among the blocks in i through j is N! / (j — i + 1). That's because there's N! total permutations, there are j — i + 1 blocks in that section, and by symmetry each of the blocks appears first in the same number of permutations.
By precomputing N! / k we get an O(N2) solution. It can be sped up to O(N); maybe you can see how.
Thank you very much :)
Here, two blocks x and y ( x ≤ y ) are connected when, for all z ( x ≤ z ≤ y ), Block z is still not removed. Does it mean only blocks to the left of y are connected to it ? Can someone explain the connectivity of two blocks? or all blocks which are not removed are connected ?
Connectivity is reflexive. By “x and y are connected” they mean “x and y are both connected to each other.”
Does it imply all blocks which are not removed are connected ?
No, the condition for x, y (x <= y) to be connected is that all blocks z in the interval [x, y] should not have been removed yet. If you have three blocks 1, 2, 3 and 2 is removed, then 1 and 3 are no longer connected.
Got it. Thank you !!
Can someone explain how to solve problem B ? I'm not getting it through editorial.
It seems that F1 is solvable in O(N^4/w) with bitset and some optimizations, for example this submission.
Can someone explain the solution to task B?