ko_osaga's blog

OpenCup GP of Korea (Update: Now in Gym!)

By ko_osaga, history, 6 years ago, In English

Update 2019/01/02: The problemset is finally uploaded to CF Gym. If you didn't participated before, this is a great chance to practice on one of Petr's best problem candidates. I hope you enjoy the contest. Happy New Year!

Division 1 Link

Division 2 Link .

.

.

OpenCup GP of Korea (third edition) is scheduled at 2018/10/14 Sunday, 11:00 MSK.

Both Div1 / Div2 problemset will feature Korean problems.

Problemsetters: ainta alex9801 Cauchy_Function Konijntje jh05013 ko_osaga OnionPringles jo_on .o.

Enjoy!

Tags gp, of, korea
  • Vote: I like it
  • +104
  • Vote: I do not like it

»
6 years ago, # |
  Vote: I like it +19 Vote: I do not like it

Can you please give a link to the contest?

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

How to solve A,E,M?

→ Reply
  • »
    »
    6 years ago, # ^ |
    ← Rev. 2   Vote: I like it +34 Vote: I do not like it

    M: Trick from IOI 2016 Aliens

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      how to prove that this trick works here?

      → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        You can think of getting answers for k=1, 2, 3, ..., as computing some partial solutions in maxflow-mincost in bipartite graph formed by the tree. Even in general MFMC every following augmenting path gives you profit which is not larger than previous profit what translates to convexity of f(k) function what is what we need.

        → Reply
        • »
          »
          »
          »
          »
          3 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          How to prove that “in mcmf every following augmenting path gives you profit which is not larger than previous profit“ ?

          → Reply
          • »
            »
            »
            »
            »
            »
            3 years ago, # ^ |
              Vote: I like it 0 Vote: I do not like it

            That's one of the properties that is crucial to proving the correctness of standard approach. Please read some explanation of MFMC algo and it should be proven there (I guess if it wasn't true then you would find some negative cycle which is supposed to not exist or sth)

            → Reply
  • »
    »
    6 years ago, # ^ |
    ← Rev. 2   Vote: I like it +20 Vote: I do not like it

    A: Build heavy-light decomposition and solve for each path independently. Now we need to recolor some prefix of path and maintain for each color number of edges with this color. It can be done with stack.

    → Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +28 Vote: I do not like it

    E: Delete all multiple edges. Take some vertex of degree 2, delete it, and connect its neighbours. Do this while there is at least one such vertex. In the end check that the remaining graph is 2 vertices connected by edge.

    → Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    A: Use heavy-light decomposition. Now every update introduces at most one new point where the color changes in each of the O(log(n)) paths. Therefore we can afford to keep track of all segments with the same color.

    E: Keep removing nodes of degree 2 until only a single edge remains.

    → Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

How to solve G?

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +1 Vote: I do not like it

    You can see the solution in the attached PDF.

    I can't believe that this was solved by 58 teams. This is intended to be the medium-hard level in this GP.

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it +18 Vote: I do not like it

      I've seen this problem a couple of times

      → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it +13 Vote: I do not like it

      I remember that there was a similar problem in Open Cup (swap K times and do something for an array, solve it in O(Npoly(K))), but I can't find the link now.

      → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
          Vote: I like it +8 Vote: I do not like it

        I see. There was some notorious coincidence :(

        → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      We just wrote O(nk3) solution with array rotation hoping that caching would help. Work like a charm.

      → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it -10 Vote: I do not like it

      I've just read this problem and I think I haven't seen anything similar but I knew how to solve it immediately after reading the statement (which was not the case for any other problem I've read from this contest (ABCEIJKM)) and I think it was similar for Marcin who solved it in my team. I think it's rather you overestimating difficulty rather than half of people knowing this problem.

      → Reply
»
6 years ago, # |
  Vote: I like it +32 Vote: I do not like it

Thank you so much for participation!

Problem author:

You can see the solution for large subset of Div1 / Div2 problems, here.

→ Reply
»
6 years ago, # |
  Vote: I like it +3 Vote: I do not like it

If I don't make a mistake, C is equivalent to some generalization of Catalan numbers.

You are given points (0, h0), (1, h1), ..., (X, hX). How many ways are there to go from (0, 0) to (X, Y) by passing exactly K of these points? You are not allowed to go above the points.

How to solve it (in quadratic time)?

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +28 Vote: I do not like it

    All surviving hands will be to the left of all surviving flowers. Also, the rightest surviving hand will be adjacent to the leftest surviving flower. If we fix this position, then the problems for prefix and suffix become independent and also on prefix we only care about A and on suffix we care about B. Let li, j be equal probability that if we start with prefix i and j hands coming from the right, in the end there will be exactly A hands and no flowers. We can define ri, j similarly for suffixes and flowers. Then the answer is .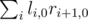

    → Reply
»
6 years ago, # |
  Vote: I like it +11 Vote: I do not like it

Will it be possible to share test cases: M15, M22, M35? Slightly different implementation of Alien trick gets WA in these cases.

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +18 Vote: I do not like it

    We have WA35 because of small INF in binary search.

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      You are right. Taking MaxW gives WA35. Taking some big number, may be N*MaxW gives AC. Why? I thought MaxW is enough.

      → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Line graph with cost ∞,  - ∞, ∞,  - ∞, ..., ∞

        → Reply
        • »
          »
          »
          »
          »
          6 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          We had taken 3MaxW. So: W, -W, W, ... -> 4W, 3W, 4W .. should not be problem right? It will rightfully pick all 4W's.

          → Reply
          • »
            »
            »
            »
            »
            »
            6 years ago, # ^ |
              Vote: I like it 0 Vote: I do not like it

            I don't understand what you are talking about, but in those cases, f(X) =  - X × W, f(X + 1) = (X + 1) × W. There is no way f(X + 1) could be found, when the range of binary search is O(W).

            → Reply
            • »
              »
              »
              »
              »
              »
              »
              6 years ago, # ^ |
                Vote: I like it 0 Vote: I do not like it

              I see, my sign was opposite, so for me the anti case was -inf, inf, -inf...

              → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        I also use MaxW+10 and got WA35 and don't know why it is not enough. :(

        → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      We had WA9 because of small INF in ternary search (I thought optimum might be non-integer even if the answer obviously is). I felt that there must be binary search solution too but couldn't figure it out. I just used standard approach — try to reduce problem to integer linear problem; check if integer requirement can be thrown out; if it is, construct a dual problem and solve it. In this case dual problem can be easily solved if one parameter (dual to the number of edges equality) is fixed. Since we have linear programming, the function must be convex and so I used ternary search to optimize this parameter.

      This looks similar to the binary search solution but I don't understand how the connection works in general case. Is it some kind of partial-dual trick?

      → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Can you please more elaborately explain how you throw out integer constraint? Or Any link to a problem using same technique?

        → Reply
        • »
          »
          »
          »
          »
          6 years ago, # ^ |
            Vote: I like it +5 Vote: I do not like it

          It is called a relaxation.

          I try to prove that optimum solution has integer values. In this case equations are organized in a tree and all their coefficients are +-1 and so it can be easily seen that any non-integer optimum can be converted to an integer optimum in this problem.

          Another example of this idea is the assignment problem. If you have non-integer solution, you can construct a cycle of non-integer edges. The move half of them one direction while moving the other half in the opposite direction until one of edges hits 0 or 1 and number of non-integer edges decreases. This proves that any linear programming solution of the assignment problem either has integer coordinates or is equivalent to a solution with integer coordinates. This point of view explains where potentials in assignment algorithms come from — they are dual variables for linear programming formulation.

          → Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Btw, you can now download tests here. (600MB)

    → Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

How to upsolve problems from div-2? Link on opencup.ru is broken and contains empty contest_id.

→ Reply
»
6 years ago, # |
  Vote: I like it +10 Vote: I do not like it

How solve K?

→ Reply
  • »
    »
    6 years ago, # ^ |
    ← Rev. 3   Vote: I like it +10 Vote: I do not like it

    UPD: Same but faster solution is described by ko_osaga below. My one has an extra factor and may get TL.

    Forget about the starting position for a moment.

    Assume we've just taken the drug at position i and it was Ci-th in order. That means that either the whole segment [i - Ci + 1, i] is taken, or the whole segment [i, i + Ci - 1]. Let us do the backward DP over such segments: d(l, r) equals to the maximum amount of damage we can get if we have eaten all drugs from l to r. Transition: d(l, r) = maxl', r'd(l', r') + last_drug, where l' ≤ l < r ≤ r', and last_drug is the score of eating the drug that gave us the segment [l, r].

    Now we consider all segments in decreasing order by their size and compute the DP using some 2-dimensional data structure. Finally, the answer for the initial problem when we start at the position i is d(i, i), that is, the maximum DP value over all segments such that l ≤ i ≤ r.

    You must be careful with off-by-one errors: when considering [i - Ci + 1, i], you should take maximum over segments covering [i - Ci + 1, i - 1] and store this value into dp(i - Ci + 1, i). This stopped me from accepting the problem at the last minute.

    P.S. Curious fact: I don't know how to solve the problem for a single starting point faster than for all of them at once.

    → Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +10 Vote: I do not like it
    Spoiler
    → Reply
»
6 years ago, # |
  Vote: I like it +23 Vote: I do not like it

How to solve B?

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +15 Vote: I do not like it

    (by ilyakor)

    Let's find strongly connected components of cells. Now each star can be attributed to at most two SCCs: one corresponding to the cells going the most to bottom and top from it, and one corresponding to cells the most to left and right from it.

    Now the problem is: we have a new acyclic graph (of SCCs), and need to find a path that passes through at least one vertex in each star pair. This can be reduced to 2-SAT if we say that a set of vertices belongs to a path if and only if it doesn't have two "incomparable" vertices.

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it +15 Vote: I do not like it

      I guess the same can be done without SCCs directly via 2-SAT: each star gets a boolean variable depending on whether we pass it horizontally or vertically, and we get constraints that prohibit using two segments such that neither can be reached from the other one, and also prohibiting segments not reachable from the start.

      → Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

What is the solution of game on plane?

→ Reply
»
6 years ago, # |
  Vote: I like it +3 Vote: I do not like it

What’s the idea behind Div2 L (Timsort)?

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    If you preprocess the next position of each i, you can answer one query in O(N / MINRUN) and save the result for that MINRUN. Doing this, the worst case is when the queries are 2, 3, 4, 5 ... N, but this is (N / 2) + (N / 3) + ... + (N / N) which is of order O(N log N). If you don't save the result after each new query and the queries be 2, 2, 2, 2..., the solution is O(N^2).

    → Reply
»
6 years ago, # |
  Vote: I like it +31 Vote: I do not like it

Is it possible to upload the contest to Codeforces?

→ Reply
»
6 years ago, # |
  Vote: I like it +8 Vote: I do not like it

Auto comment: topic has been updated by ko_osaga (previous revision, new revision, compare).

→ Reply
»
6 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

Edit: It is on vjudge already. Thanks!

Hi ko_osaga, do you mind to invite vjudge accounts (vjudge1, vjudge2, vjudge3, vjudge4, vjudge5) to this gym contest, so vjudge users can create contests with these awesome problems. Thanks!

→ Reply