usernameson's blog

What's the deal with 998244353?
By usernameson, history, 6 years ago, In English

I have noticed that educational rounds like to use mod 998244353 instead of mod 109 + 7. Does anyone know the reason for this? One idea that comes to mind is since 998244353 < 109 there might be opportunities to troll contestants by breaking division and forcing them to calculate things like 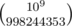mod 998244353. However I have yet to see this used in an educational round, although this idea was used to good effect in 272D - Dima and Two Sequences.

  • Vote: I like it
  • +11
  • Vote: I do not like it

Comments Comments (14)
| Write comment?
»
6 years ago, # |
  Vote: I like it +10 Vote: I do not like it

As far as I know, 998244353 allows you to do interesting stuff related to polynomial multiplication I haven't fully studied yet. See this CF tutorial and this note in Petr's blog.

Other times, 998244353 is used because it's prime, much like 109 + 7, or 109 + 9, or 106 + 69. There can also be a mind-game factor involved: one time, I thought a problem needed the above tricks to be solved simply because the modulo was 998244353, but in the end, I was fooled!

Why it appears often in educational rounds? I don't know, you'll have to ask the setters for that.

→ Reply
»
6 years ago, # |
  Vote: I like it +53 Vote: I do not like it
998244353 = 1 + 7·17·223.

This is nice because it lets you do Fast Fourier Transforms (mod p) using only the integers. In other words, the setters don't want to give away whether the problem is supposed to be done using FFT or not.

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +15 Vote: I do not like it
    the setters don't want to give away whether the problem is supposed to be done using FFT or not.

    I think FFT can be done even with modulo 109 + 7. You can do it by FFT with some large two modulos, for example, modulo 1 + 7·226 and 1 + 5·225. Then you can restore the value using Chinese Remainder Theorem (or extended Euclidean algorithm). And finally modulo it by 109 + 7.
    Obviously, this way also works for 109 + 9, 998244353, or some other modulos. But, if the modulo is 109 + 7, I think that some people may think "the solution is definitely not FFT" even if FFT is actually involved. Finally, I think taking modulo with 109 + 7 or 109 + 9 is the best way to hide the solution (whether FFT or not).

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it +13 Vote: I do not like it

      Recently, problem setters found that giving every problem modulo 998244353 is the best way to hide the solution :( Now 998244353 doesn't mean anything. There are so many problems not using FFT but having modulo 998244353...

      → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it +15 Vote: I do not like it

      Sorry, I wasn't necessarily talking about polynomial multiplication: I agree you can do CRT to do polynomial multiplication mod 109 + 7 say. 998244353 is special because you can actually do a fourier transform with a 2n-th root of unity.

      Also, I would say that I also agree that it's just more convenient to have a template to do polynomial multiplication modulo p for any prime p.

      → Reply
  • »
    »
    5 years ago, # ^ |
      Vote: I like it -26 Vote: I do not like it

    desert97 Can you explain what you meant?

    → Reply
»
6 years ago, # |
  Vote: I like it +1 Vote: I do not like it

I wonder what people will do if I invent an algorithm which only works on mod 696969420...

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +21 Vote: I do not like it

    People won't do this problem since they will get the ultimate orgasm with the first glance.

    → Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +13 Vote: I do not like it

    Just imagine what will happen if people realize there were already some good problems about mod 2!!

    → Reply
»
5 years ago, # |
  Vote: I like it -11 Vote: I do not like it

usernameson Did you find the reason?

I guess the reason to use 998244353 instead of 10**9+7 is that this hides the answer better... Can't seem to find anything else... This number has again been used in Educational Round 79 (1279D - Santa's Bot)

→ Reply
  • »
    »
    5 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    The FFT answer above made sense to me so I assumed it was correct.

    → Reply
»
5 years ago, # |
  Vote: I like it +3 Vote: I do not like it

I'm still waiting for 1000696969 to become a popular mod prime.

→ Reply
»
4 years ago, # |
  Vote: I like it 0 Vote: I do not like it

In china it's more commonly written as (119<<23)+1

→ Reply
»
2 years ago, # |
  Vote: I like it +3 Vote: I do not like it

Say my question asks mod 10^9 + 7 but I use 998244353 to take advance of the polynomial operations . Now how do I transform my answer back to modulo 10^9+7 ?

→ Reply