Задачи A-G придумал и подготовил isaf27. Идею задачи A предложил peltorator.
Задачу H придумал и подготовил cdkrot.
Tutorial is loading...
Решение жюри: 44522356
Tutorial is loading...
Решение жюри: 44522430 Tutorial is loading...
Решение жюри: 44522470 Tutorial is loading...
Решение жюри: 44522488 Tutorial is loading...
Решение жюри: 44522506 Tutorial is loading...
Решение жюри: 44522527 Tutorial is loading...
Решение жюри: 44522542Решение Endagorion: 44519413 (максимальный остов)
Tutorial is loading...
Решение жюри: 44522571










A bit different approach for D: lets build the answer greedily. On each moment add value, which will minimize the number of bad segments ( when current prefix is equal to some previous). lets just pick best for it.
code
in the end it goes almost to the same solution.
Could you please elaborate why this is working?
Почему нет перевода?
Скоро появится
Auto comment: topic has been translated by isaf27 (original revision, translated revision, compare)
When editorial will be available in English
Soon
Use Google Translator
Google translate has certain problems while displaying mathematical things.
Time to learn some russian I guess.
If you wanna know how to solve H easily using FFT, you can read my blog entry explaining a very simple FFT implementation.
FFT made easy
Editorial for problem D is in Rusian! I dont understand :(
OK, I'll try to explain in Spanish then.
La solución es con prefijos de xors. Suponé que vas a procesar la posición i. Tenés dos opciones, o agarrás Ai o agarrás el complemento de Ai. Fijate cuál apareció menos veces en los prefijos que ya pasaron y usá esa. Es greedy la solución. Pasa.
arigatou!!!
Please post editorial in English as well.
Now editorial is available. Sorry for waiting.
Here is a linear time solution for H that doesn't pass any tests (I'm just writing it here because I think it's cool).
Consider the polynomial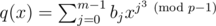 , where the modulo in the exponent is OK because of Fermat's little theorem. Then the degree of q(x) is at most p - 1. Say we could compute ti = q(ci2) for all i = 0, 1, ..., i - 1. Then we would be set, because then the answer is simply
, where the modulo in the exponent is OK because of Fermat's little theorem. Then the degree of q(x) is at most p - 1. Say we could compute ti = q(ci2) for all i = 0, 1, ..., i - 1. Then we would be set, because then the answer is simply 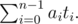
There is an algorithm that does polynomial multi-point evaluation (exactly the thing stated) in time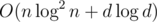 where n is the number of points and d is the degree of the polynomial. This would give a "linear" time solution, except it runs way too slowly.
where n is the number of points and d is the degree of the polynomial. This would give a "linear" time solution, except it runs way too slowly.
I actually mentioned it in my earlier comment, but I also wrote there how to solve problem in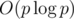 to find all values of some polynomial P(x) modulo prime number p for all numbers 1, ..., p - 1.
to find all values of some polynomial P(x) modulo prime number p for all numbers 1, ..., p - 1.
And multipoint evaluation in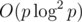 was intentionally cut out by authors.
was intentionally cut out by authors.
In problem H, you can also handle all three components simultaneously by applying FFT to the 491 and 499 dimension and FWT to the 2 dimension.
See my code here if necessary.
After all, problem H is such a fantastic problem that I really enjoyed it.
Can anyone please explain the solution to Problem D?
The solution relies on two/three ideas:
First idea:
So basically we can observe a xor a = 0. This is because every digit is the same, and thus each position becomes 0. And that a xor 0 = a. We can use this to get range xors in O(1). For example: (xor of a[1..R]) xor (xor of a[1..L-1]) = xor of a[L..R] because elements from 1 to L-1 get cancelled out.
Second idea:
And let us define comp(x) as flip the first k bits of x and return it. Well then comp(x) = x xor (2^k)-1, because 2^k-1 stores all 1 which will flip each bit. And by definition of xor (add each digit and mod 2), it is commutative and thus it don't matter when you xor by (2^k)-1.
Third Idea:
Let us define p[i] = a[1] xor a[2] ... xor a[i]. So by definition of problem we can always set the array a[i] to comp(a[i]). But by our previous definition of comp(x), we can see it something like comp(a) xor b xor c = comp(a xor b xor c). So xor'ing position i will affect p[i+1], p[i+2] and so on. But if you xor position i+1 it will cancel the effect. Therefore we can arbitraily set p[i] to comp(p[i]) by doing xor on a[i] and then again on a[i+1].
Now this leads us to the solution. For every value X in the array have an "corresponding" value of comp(X), which we can interchange by definition of the problem. We only want one of them, say, the minimum. (other methods of separating works).
Then for each we assign roughly half of X to comp(X) so to minimize repeat occurences of X in the prefix xor sum (p[i]). Why? Because (a xor a) = 0, and thus it is a bad subarray.
We can count the answer fast now using formula. N positions * N-1 other positions / 2 because we both consider (A -> B) and (B -> A) gives us formula cnt(cnt-1)/2 bad positions if there are cnt amount of element X in the result array.
Can anyone explain why the O(n3) solution of F run such fast ?
IN D:
min(pi,(pi)')
why we take min??
We could also take max, or number with most/least one bits, or anything else that always divides numbers into two categories: the basic idea is that we don't want pi and (pi)' to both be counted, only one of them.
In the case we take max, treat the 0 index as (1<<k)-1 instead of 0.
My code: 44885325
Edit:
Of course, you don't need to even use some separating function. Instead you can count the solution twice by calculating bad sequences for x with the sum of the count of x and x'. But then you subtract twice the amount, so you need to account for overcount. (i.e divide subtracted amount by 2)
please anyone explain solution of c
Even though I am just restating editorial, hope it helps
Let's first ignore the whole L an R thing. Instead we can make array, let's say, g[i] where as position i there are g[i] other element greater than it. Well g[i] = L[i] + R[i].
Now we can also observe that if (elements > x) + (element <= x) = n
Well that means g[i] + (element <= x) = n, and thus the amount of elements less than or equal value at position i = n-g[i] = (n-L[i]-R[i]).
Now let us say there are k elements less than or equal to than the current element (one of the k elements may be the current element itself). If L and R are valid then then you can just assign current element as k. So ans[i] = (n-L[i]-R[i]).
If L and R are consistent by definition it will always be an answer. If the L and R is not valid, when you check this resulting array, there will be problems so we can say it is impossible