Mail.Ru Cup 2018 Round 2 — analysis

6 years ago, # ^ |

Holy crap can't believe I missed this

→ Reply

6 years ago, # ^ |

Can you please explain how Bezout's identity can be used to prove the above point ?

→ Reply

tatya_bichu

6 years ago, # ^ |

← Rev. 4 →

+13

https://imgur.com/a/e8lm6rY, Look at the image, we have two patterns length of 6(123456) and 4(ABCD), shift will be 2(6-4),4(12-8),6(18-12).... so on, Also for length a and b where (a > b), shift will be of form of x * a - y * b which is a multiple of GCD(a, b), hence every shift will be a multiple of GCD(a, b)
EDIT: What is a shift here? :
Look at the image and observe the indices of starting points of patterns (1)23456 and (A)BCD , 1 has indices 1,7,13,19 and A is at 1,5,9,13,17 , so shift is the difference of indices of starting points of the patterns, 1-1 =0, 7-5 =2, 13-9 =4 and 19-13 =6 ... so on

→ Reply

rahul1995

6 years ago, # ^ |

what is a shift??

→ Reply

6 years ago, # ^ |

Imagine as stacking on:

In the first stack: we adds pieces of size 4.

In the second stack: we add pieces of size 6.

If we add same amount to both, the second stack will get 2 more ahead each piece added.

→ Reply

6 years ago, # ^ |

Thanks a lot. :)

→ Reply

6 years ago, # |

← Rev. 5 →

+20

I solved problem D just after the contest, but I thought a little about my solution and found that it's wrong. Suppose next test:

2
xax
yay
xbx
ycy

Which answer would you prefer? "NO" or "YES a b"? My accepted solution 45540070 said "YES a c", but the strings won't be equal after applying this operation.

In other words, when i'm looking for the leftmost and rightmost indexes where strings s and t differ, I check that s[i] != t[i]. After that I check that substring of s is the same in all the strings where any characters differ, but I never check that strings t taken with the same indexes are equal.

→ Reply

6 years ago, # ^ |

← Rev. 2 →

Jacob please reply. I don't think it's ok.

→ Reply

6 years ago, # ^ |

+20

I agree it's not ok, sorry about this. We somehow overlooked this opportunity to make a bug and didn't prepare tests against it. I have added your test to the upsolving.

→ Reply

6 years ago, # ^ |

← Rev. 3 →

-12

Don't you wanna rejudge all the submissions? I'm sure I'm not the only who missed this.

→ Reply

6 years ago, # ^ |

-31

Kuyan, Jacob, cdkrot, 300iq, MikeMirzayanov, I'm waiting for any response about rejudging.
I know it won't affect final standings much, but anyway there may be incorrect solutions which got Accepted when it's wrong.

→ Reply

6 years ago, # ^ |

+21

We never rejudge submissions after the contest. I can add some tests to upsolving if you want.

→ Reply

adamant

6 years ago, # |

+26

Since the order of those values doesn't matter, let's build a binary trie of those numbers.
It's possible though to recover bits of the answer one by one by descending the trie level by level and maintaining the pairs of trie nodes that give us the correct higher bits of the answer (node may be in pair with itself).

But it gets ML immediately!! :(

Really, can you kindly explain reasons to prevent competitors from constructing trie explicitly?

→ Reply

6 years ago, # ^ |

Incidentally, my solution is just array traversal. Basically, when processing a bit, I have pairs of arrays (a, b) such that only all xor(element of a, element of b) are considered; these arrays are all concatenated and I just remember the positions where they start/end in the resulting array.

Processing bit b consists of counting how many pairs give a xor with bit b equal to 0, deciding what should be the b-th bit of the result and using that to split each pair (a, b) into 4 arrays a₀, a₁, b₀, b₁ based on the value of bit b in their elements and pairing them up, with some obvious anti-blowup rule like "skip pairs where one array is empty".

This can be implemented recursively, but also using just 2 concatenated arrays and 2 start/end-arrays for odd and even b. A convoluted approach that passes these limits...

→ Reply

6 years ago, # ^ |

Thanks for noting this, I've now added some explanation to the analysis that the trie should be constructed implicitly after sorting all numbers first.

Now I'd like to explain the reasoning behind memory limits in this problem. Some of the round testers actually prepared explicit trie solutions. Being written in C++ with rather heavy optimizations, they could pass the time limit but with a minimal margin (if ML was set to 1024Mb). Therefore, in my opinion, raising memory limit to allow explicit trie solutions would create additional "randomness" in this problem (we didn't want participants to spend too much time optimizing the correct solutions) and would give participants who code in C++ some advantage over Java (because in Java sneaking under the time limit with explicit trie is much harder, if not impossible).

→ Reply

6 years ago, # |

+13

The time limit and constraints of F really don't go well. I rewrote my clearly O(62n) algorithm using a vector<pair<vector,vector>> into one with vector<long long>, vector<pair> (the point is memory efficiency, which really shouldn't be a factor when possible) and got AC in 2 seconds instead of TLE. Yes, AC is possible, but it might need heavy constant optimisations even with a good algorithm simply because the input is big. Twice as large TL or half as large input would make it still about some constant optimisations of stupid implementations, but not such heavy ones.

→ Reply

6 years ago, # ^ |

-18

We would probably wanted to have slighly larger TL, however this makes a log² solution close to pass.

Besides, the TimeLimit was not very strict in fact. We even had the model written in java!

→ Reply

6 years ago, # ^ |

+10

Java isn't a magic constant-time slowdown. How a program works depends on what it does, not what language it's written in.

This gets TLE. The time complexity is O(62N) and it doesn't use any special STL functions, apart from vector<> push_back and copy-constructor. You don't have to explain to me why it gets TLE, but you could explain if that's intended to fail.

→ Reply

6 years ago, # ^ |

-18

Yes, we found that during testing. We believe that the constant factor of this implementation of the solution (unfortunately) is so large that it is even not very much possible to cut it from O(log²).

→ Reply

6 years ago, # ^ |

-18

There is some slightly other approach however, which doesn't have so many memory operations.

→ Reply

6 years ago, # ^ |

+10

Yeah, my "slightly different approach" is just working with a concatenation of all those arrays + vector of their (start, end) pairs instead. Still, understanding why this works is something I consider beyond the scope of a sane problem in an algorithmic contest — I only learned about such things when I started working. It's not super difficult knowledge, but tangential knowledge.

That's the problem with trying to distinguish between log and a constant in competitions. In my experience, it's not worth doing because you'll only end up with this situation — people passing because of an implementation they chose by chance. The same applies to strict limits in interactive problems. Of course, there are exceptions, but they're very specific and usually just see that it's a problem where you can push things further.

I'm not even outright opposed to constant factor being a factor (lol), but when it's clear that a constant matters, it's best to admit it and put a warning in the statement or something.

→ Reply

adamant

6 years ago, # ^ |

+10

Why is it the third problem I encounter during last month, with your involvement in its preparation and which has such kind of issues?..

Reminder: 1054H - Epic Convolution, 1043D - Mysterious Crime

P.S. I suppose it would be enough to just lower numbers to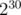 $\text{[math]}$ to both still cut off binary search and 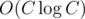$\text{[math]}$ solutions, but not cut off 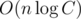$\text{[math]}$ memory and not have such constant-optimization issues... Am I wrong?

→ Reply

6 years ago, # ^ |

← Rev. 3 →

-8

I agree, that you have a point on 1043D, it was not very nice indeed

As far as I've seen, you are wrong about 2³⁰

→ Reply

ganariya

6 years ago, # |

I'd like to ask about C problem.I'm dense, sorry. I thought that ta and tb is LCM, in the contest. Why is gcd, not lcm? I think that lcm is because ta and tb are period. Thank you.

→ Reply

http://codeforces.net/blog/entry/63099?#comment-470272

6 years ago, # ^ |

← Rev. 3 →

LCM also works, but GCD is more useful to us. It's not too difficult to see why you would repeat every LCM tiles. But here is intuitive way to show GCD will work.

First define A' = A/gcd(A,B) and B' = B/gcd(A,B) and now realize lcm(a,b) = A' * B' * gcd(A,B)

And now group your data into chunks of size gcd(A,B), and you will notice every A' * B' chunks will repeat.

xo|oo|oo|xo|oo|oo|(repeating) here x's are 6 apart

xo|oo|xo|oo|xo|oo|(repeating) here x's are 4 apart

A |B |C |D |C |B | (repeating) the pattern ABCDCB will repeat (what I decided to label chunk patterns as)

(Try writing it out and drawing lines at every gcd(6,4) = 2 characters away, A'*B' = 6)

But actually it doesn't matter what A'*B' is, we only care that the pattern can be contained within gcd sized chunks. Because it can, we can just move down both left indices to the first chunk (say, by doing l=l%gcd) while maintaining correct bounds

This is actually enough observation to pass the tests: https://codeforces.net/contest/1055/submission/45546142 (ignore the weirdness of the gcd function, just leftovers from another idea)

→ Reply

tatya_bichu

6 years ago, # ^ |

I think, if you use lcm you'll get the interval after which patterns get same corresponding values, if you use lcm instead of gcd , shifts will not have any effect

→ Reply

sajid006

6 years ago, # ^ |

Can you tell me what does shift mean?

→ Reply

tatya_bichu

6 years ago, # ^ |

→ Reply

neal

6 years ago, # |

+13

The solution for F described here is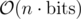 $\text{[math]}$ . Was it intentional for the hash map solution of the same time complexity to time out?

→ Reply

aid

6 years ago, # ^ |

+11

Hash map has big constant. My solution(45530383) is the same as yours, but I use sort instead of hash map. Asymptotically it is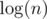 $\text{[math]}$ times slower but in practice it is faster.

Overall I think trying to not let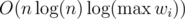 $\text{[math]}$ solutions pass in this problem is bad, because the difference in time is not big enough.

→ Reply

neal

6 years ago, # ^ |

+10

My final in-contest submission did the same: 45535363. Unfortunately while your code was just under 4000 ms, mine ended up barely over the limit. The same code passes by adding fast I/O to save a few hundred ms: 45571940. Agreed on the difference not being big enough.

→ Reply

6 years ago, # ^ |

-20

The intention of rather severe constraints and time/memory limits here was to differentiate the binary search from the solutions with the correct (intended) complexity, because the binary search in this problem is probably too simple. In our case a reasonable (not very optimized) solution in Java implemented in the way described in the analysis worked in about half of the time limit, and significant part of that was just I/O. There is also an obvious room for 2x speedup in the actual computation by exploiting the symmetry and reducing the number of states in half. This means that likely your solution indeed has a very high constant factor.

→ Reply

6 years ago, # ^ |

← Rev. 2 →

Representing a trie node by a range of indices in a sorted array is a heavy optimisation.

In detail: depends on implementation, but it will most likely have an extremely low number of cache misses, pipeline stalls and write buffer stalls (if the architecture has write-through cache). If trie nodes were actual node pointers, it would be much worse.

→ Reply

neal

6 years ago, # ^ |

+18

I think it's acceptable to distinguish linear from log-linear. However, in practice what actually happened here is that many linear solutions failed, and some log-linear solutions still passed, so in the end it really just became a constant factor contest.

→ Reply

Vladislao

6 years ago, # |

+50

Just because there are people that want to know more about problem C and that the editorial isn't very eloquent, I'll give a more detailed analysis.

First of all, if one can make an Alice's interval and a Bob's interval coincide (in the sense that both begin in the same number) then the answer is just min(r_b - l_b + 1, r_a - l_a + 1) (the length of the shortest interval).

However, this may not be possible (for example, if Alice's pattern is +++--- and so on, and Bob's are -+++-- and so on, they will never begin at the same place).

Something important is to remark that in particular in a "maximal overlap" one of the intervals beginning will be inside the other full interval (it means that Bob's beginning lies on an Alice interval, or the opposite).

So let's analyze what happens with a maximal overlap in the case that Alice's interval beginning lies on Bob's interval (note that Alice's interval may be longer or shorter than Bob's).

The only possible values for Alice's beginning are of the form l_a + kt_a, and in particular, we want to know the least possible value of y such that l_b ≤ y ≤ r_b and that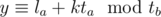 $\text{[math]}$ .

Note that for such an y to exist, it's neccesary that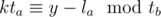 $\text{[math]}$ . And as k is immaterial at this point, this means that the congruence 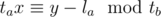$\text{[math]}$ has to be solvable, which means that 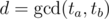$\text{[math]}$ must be a divisor of y - l_a. So, we want to know the least y in the interval [l_b, r_b] such that y - l_a is divisible by d.

The naive approach would be to iterate from l_b to r_b, but this is very slow in the worst case. But if one calculates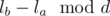 $\text{[math]}$ one can see how many steps are needed to achieve a $\text{[math]}$ .

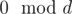Once this y is calculated, as we pointed at the beginning of the comment, one has to calculate the minimum between r_a - l_a + 1 (Alice's length) and r_b - y + 1 (the "remaining" part of Bob's interval).

Of course, then one has to proceed interchanging the roles of Alice and Bob, and then print the maximum of the two calculated values.

→ Reply

6 years ago, # ^ |

← Rev. 2 →

" ...the congruence has to be solvable, which means that d = gcd(ta, tb) must be a divisor of y-la" . How did you reach this conclusion about d ?

→ Reply

poojanpatel101

6 years ago, # ^ |

First common point in two ap.
https://math.stackexchange.com/questions/1656120/formula-to-find-the-first-intersection-of-two-arithmetic-progressions

→ Reply

6 years ago, # ^ |

Thank you very very much. :)

→ Reply

6 years ago, # ^ |

$\text{[math]}$ , so kt_a + ht_b = y - l_a and $\text{[math]}$ divides the left hand side.

→ Reply

6 years ago, # ^ |

Thanks. :)

→ Reply

amstan

6 years ago, # ^ |

I understood the whole idea but just need a little bit more clarification over the line

"if one calculates one can see how many steps are needed to achieve 0 % d"

Can you please tell me that it calculates the smallest y that is in the range [lb,rb] such that d|(y-la) ??

i.e. y=(lb-la)%d ?

→ Reply

wzm

6 years ago, # ^ |

if (lb - la)mod5 = 2, it needs 3 steps to make ((lb + 3) - la)mod5 = 0

→ Reply

asvasil

6 years ago, # |

Should there be the word "multiset" in the problem E statement?

→ Reply

VLADO

6 years ago, # |

← Rev. 2 →

Can someone explain the O(log N) solutions for C some people had?

→ Reply

Jostic11

6 years ago, # ^ |

I'm not sure I can explain, but maybe you're wrong. in the analysis told the solution for log (N) (gcd works for log)

→ Reply

VLADO

6 years ago, # ^ |

Oops yeah gcd works in log N... still I meant the solutions that for example the top 5 people submitted, they don't look like the solution explained in the editorial

→ Reply

matcoder

6 years ago, # |

Can someone post a more detailed solution of problem D ? I am still not able to catch the core idea to crack the problem...

→ Reply

6 years ago, # ^ |

← Rev. 2 →

-10

Sorry if the analysis is a bit unclear. I can give some example:

Suppose you need to rename variable "ababaca" to "abcbdca". The core of the replacement is "aba"-"cbd". If this is the only variable that you need to change, you may expand the pattern to the left ("ab") and to the right ("ca").

If you have another variable "cbabacaba" that you need to rename to "cbcbdcaba", then the right expansion may remain the same (because in this variable there is also "ca" to the right of the core), but to the left you need to shorten your expansion to "b". So now after this your replacement pattern looks like "babaca"->"bcbdca".

→ Reply

matcoder

6 years ago, # ^ |

Thanks for replying. Please edit 2nd variable replaced name as "cbcbdcaba" instead of "bcbdcaba". What would be the proceeded approach in case where you had one more variable "babaca" with replacement same as original string that is "babaca"?

→ Reply

6 years ago, # ^ |

On the first pass if you encounter the variable that does not need to be renamed, then you just skip it. Later when you verify that you found the solution (the second pass) you will of course need to check that this variable doesn't match the pattern that you constructed.

→ Reply

matcoder

6 years ago, # ^ |

← Rev. 2 →

Cool...I got it...Thanks

→ Reply

manish_joshi

6 years ago, # |

← Rev. 4 →

+19

Here is a more intuitive and simple explanation for solution to Problem C which i found after struggling for a day,

Pre-requisite : Understand what we have to do

First of all, if one can make an Alice's interval and a Bob's interval coincide (in the sense that both begin in the same number) then the answer is just min(r_b - l_b + 1, r_a - l_a + 1) (the length of the shortest interval).

However, this may not be possible. Sometimes it isn't possible for them to perfectly overlap ever(think about it, if you don't get it, continue reading anyway).

We intend to choose lucky intervals(one of alice, one of bob) so as to minimise the difference of the start points of the intervals of alice and bob. Now convince yourself that this will give maximum intersection.

Now the easier part, the solution :)

Consider the start points of two general intervals (one of alice, one of bob).

For alice, start point of general lucky interval is : l_a + k₁ * t_a

For bob, it is : l_b + k₂ * t_b

Difference of start points, diff = l_b- l_a + (k₂ * t_b) - (k₁ * t_a)

Now, I want you to focus on last two terms of the above expression, they are : (k₂ * t_b) - (k₁ * t_a) where k₁, k₂ are general integers. That's a linear combination of t₁ and t₂ which always happens to be a multiple of gcd(t_a, t_b). In fact any multiple of gcd(t₁, t₂) can always be written as a linear combination of t₁, t₂(see Bezout's lemma for both these facts).

So we can say that the difference is of the form :

diff = l_b- l_a + k * gcd(t_a, t_b), where k is yet another integer.

We intend to minimise the absolute value of diff; so we solve the equation, diff = 0(minimise diff) for k. (Note that it may be not be possible for integer value of k, i'm coming on it)

We get after rearranging,

k = -(l_b- l_a) / gcd(t_a, t_b) (Don't do integer division here).

Of course, since diff = 0 isn't always possible because the start points of alice and bob may never overlap. So this k we have here must be calculated as a float value (use long double), its floor and ceiling are two integer candidates one of which will make the diff value minimum.

So with ceil(k) and floor(k), we obtain two different diff values. For both of these diff values, we calculate the intersection length of intervals [l_a;r_a] and [l_a + diff; l_a + diff + (r_b — l_b)] and print the maximum intersection length for two diff values. (If you don't get this last part, think about it, it's easy, you can ask if you don't get it)

You can refer to my solution here. 45568612

→ Reply

GreatBlitz

6 years ago, # ^ |

Thank you so, so much — this was helpful, I think I finally have an understanding of the problem.

If you are aware, can you recommend a few more problems on Bezout's lemma? It is the first time I have encountered this topic, and I would like to practice it more.

→ Reply

DragoonXi

6 years ago, # ^ |

Thanks for your briefs. However, even this ceil/floor trick works here (and lot of other places), i think it isn't required and we can do it neatly in one computation. It would be great if anyone can tell how to do it? My implementations are getting WAs.

→ Reply

manish_joshi

6 years ago, # ^ |

I believe it would be possible. One approach i thought was to binary search for this k(linear search might timeout). But it was adding extra complexity and extra debugging required. If anyone has a neater way, please share it.

→ Reply