Ahnaf.Shahriar.Asif's blog

Range update and point query in segment tree ?
By Ahnaf.Shahriar.Asif, history, 6 years ago, In English

Recently I have to solve a problem like : given an array, update n times in range [Li..Ri] and then output the array .I updated them using segment tree and I found the array by querying indexes one by one. It took nlog(n). Can I do it in O(n) ? And additionally, can I find the condition of any index in O(1) ? Thanks in advance.

  • Vote: I like it
  • +3
  • Vote: I do not like it

»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Assuming update means add x to every element in a range. This can be done in O(n) using an array who's prefix sums are the final array. Adding x to a range then requires two point updates at Li and Ri + 1. At the end, compute the prefix sum to get the original array.

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Is it possible to do this in O(n) for non-invertible operations? Offline range assignment in O(n) doesn't seem to be easy.

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      I don't think so. If you're curious, then if the operation is, say, that for each update (l, r, x), you need to ensure maxl ≤ i ≤ r(ai) = x, and if the updates are sorted by x (or if you can sort them in linear time), then you can solve the remaining part in .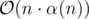

      Almost constant, but there are a couple of conditions you need anyway.

      → Reply
    • »
      »
      »
      6 years ago, # ^ |
      ← Rev. 3   Vote: I like it +11 Vote: I do not like it

      You can do offline range assignment by DSU in (n + q)·a(n). Let's process assignment queries in order from last to first. Let's say that initially all elements have white color. To process a query, we will take all elements, that are still white, from this query segment and repaint them into black, simultaneously setting their values. So for each element we will set its value only once, black element means that we already set it, and white — that this element so far didn't get into any of queries segments (remember, we process queries from last to first).

      To do this, we need to support two operations:

      • find first white element right to some position,
      • repaint white element to black.

      Let's maintain in our DSU that each white element and possibly empty segment of black elements preceding him form a separate set. So for the first operation we just need to know to which set our position belongs. And second operation is just a union of two sets: this white element's one and his right neighbour's one.

      → Reply
»
6 years ago, # |
← Rev. 3   Vote: I like it 0 Vote: I do not like it

For sums what arknave mentioned is nice.

Another idea I bring is for min/max. You don't need segment tree. You can actually just sweep and maintain a set.

Update in O(1) like this:

start[L].push(value)

end[R].push(value)

Now sweep in O((n+q)log(n+q)) like this:

Spoiler

Don't think there is anything "truly O(n)" though, the best you can get is a dsu solution (if you consider that O(n)).

→ Reply