proofbycontradiction's blog

Why use Splay Trees?
By proofbycontradiction, history, 6 years ago, In English

In programming contests, I see that many of the codes that require an implementation of a balanced BST actually use a splay tree. Why do you use them over other trees that offer stronger guarantees such as AVL trees and Red Black?

For example, see this solution by tourist.

Are they that much faster than other trees (like quicksort or binary search trees)? Or do they have some interesting non-trivial properties that are especially useful? What I mean to ask is if there are questions where using a Splay Tree gives a much better result than using other kinds of trees.

  • Vote: I like it
  • +23
  • Vote: I do not like it

Comments Comments (6)
| Write comment?
»
6 years ago, # |
  Vote: I like it +11 Vote: I do not like it

Faster than Treap, allows efficient Split / Merge operations, surely shorter than Red Black Trees and probably shorter than AVL Trees if you also want to add Split and Merge operations (which are a little more involved for AVL Trees)

I think this is definitely enough but I'm not aware of other advantages :)

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    What are split and merge operations?

    → Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +26 Vote: I do not like it

    Well I'm not sure that Splay Tree is faster than Treap, although I can't say I write optimized splay trees. I have tried solving some problems with both and always the treap solution was faster. Some of those problems were even related to Link/Cut trees.

    One advantage of splay trees is that if we use it for Link/Cut tree, the complexity will be amortized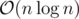 , while if we use treaps, AVL or Red Black trees for that, the complexity will be .

    → Reply
»
6 years ago, # |
  Vote: I like it +43 Vote: I do not like it

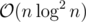Ask Darooha

→ Reply
»
6 years ago, # |
  Vote: I like it +26 Vote: I do not like it

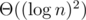There are quite a few applications such as merging (as in merge sort, not as in concatenation) and link-cut trees, where splay trees make it much easier to get amortized runtime instead of . (See also the section on finger search on wikipedia.)

You usually don't mind the fact that the runtime bound is only amortized. The notable exception to this is if you want persistent search trees.

Regarding speed, it would be interesting to see a micro-benchmark on different types of balanced trees. (Both with and without parent pointers.)

→ Reply