proofbycontradiction's blog

TLE with an O(n sqrt(n)) n <= 200000. C++ optimizations needed.
By proofbycontradiction, history, 6 years ago, In English

I was solving this interesting number-theory + trees problem. And I came up with an 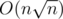solution where n ≤ 200000.

My idea is that the answer for every node will either be a factor of the root or be a factor of the number itself, and only these about 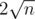values need to be tested.

However, this submission am getting TLE with this idea. The solution in the editorial is a slight optimization of my idea -
(a) either the answer is a factor of the root (because root is NOT marked as 0)
(b) or it's the GCD of all the ancestors except the root (because the root IS marked as 0).

This has the complexity of O(n * k) where k =  number of factors of the root value, and 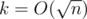. Thus the editorial solution and my solution have the same (theoretical) complexity.

Could you suggest was that are C++ implementation optimizations that I could use to improve my solution and avoid the TLE even though I am testing out both factors of root and factors of the node? I did try to cache the values of the root and the node, but that leads to a stack overflow.

I am not looking for the obvious optimizations of implementing the editorial solution.

  • Vote: I like it
  • 0
  • Vote: I do not like it

»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Auto comment: topic has been updated by proofbycontradiction (previous revision, new revision, compare).

→ Reply
»
6 years ago, # |
  Vote: I like it +3 Vote: I do not like it

Just precalculate the factors of each number 46674197.

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Ah, of course. In my solution, I was thinking about storing the factor for each node value independently (so that gives memory. I forgot that we could use sieve-like ideas for O(nlog(n)) memory.

    Thanks for your response.

    → Reply